 |
SMS701S - SURVEY METHODS AND SAMPLING TECHNIQUES - 1ST OPP - JUNE 2023 |
 |
1 Page 1 |
▲back to top |

nAmlBIA unlVERSITY
OF SCIEnCE Ano TECHn OLOGY
FACULTYOF HEALTH,NATURAL RESOURCESAND APPLIEDSCIENCES
SCHOOLOF NATURALAND APPLIEDSCIENCES
DEPARTMENTOF MATHEMATICS, STATISTICSAND ACTUARIALSCIENCES
QUALIFICATION:BACHELOROF SCIENCES IN APPLIED MATHEMATICS AND STATISTICS
QUALIFICATIONCODE: 07BAMS LEVEL:7
COURSECODE: SMS701S
COURSE: SURVEYMETHODSAND SAMPLINGTECHNIQUES
SESSION: JUNE 2023
PAPER: THEORY
DURATION: 3 Hours
MARKS: 100
EXAMINER
MODERATOR:
FIRSTOPPORTUNITYEXAMINATION QUESTION PAPER
Mr. J. J. SWARTZ
Dr. I. NEEMA
INSTRUCTIONS
1. Answer all the questions in the booklet provided
2. Show clearly all the steps used in the calculations.
3. Write clearly and neatly.
4. Number the answers clearly.
PERMISSIBLEMATERIALS
1. Calculator
ATTACHMENTS
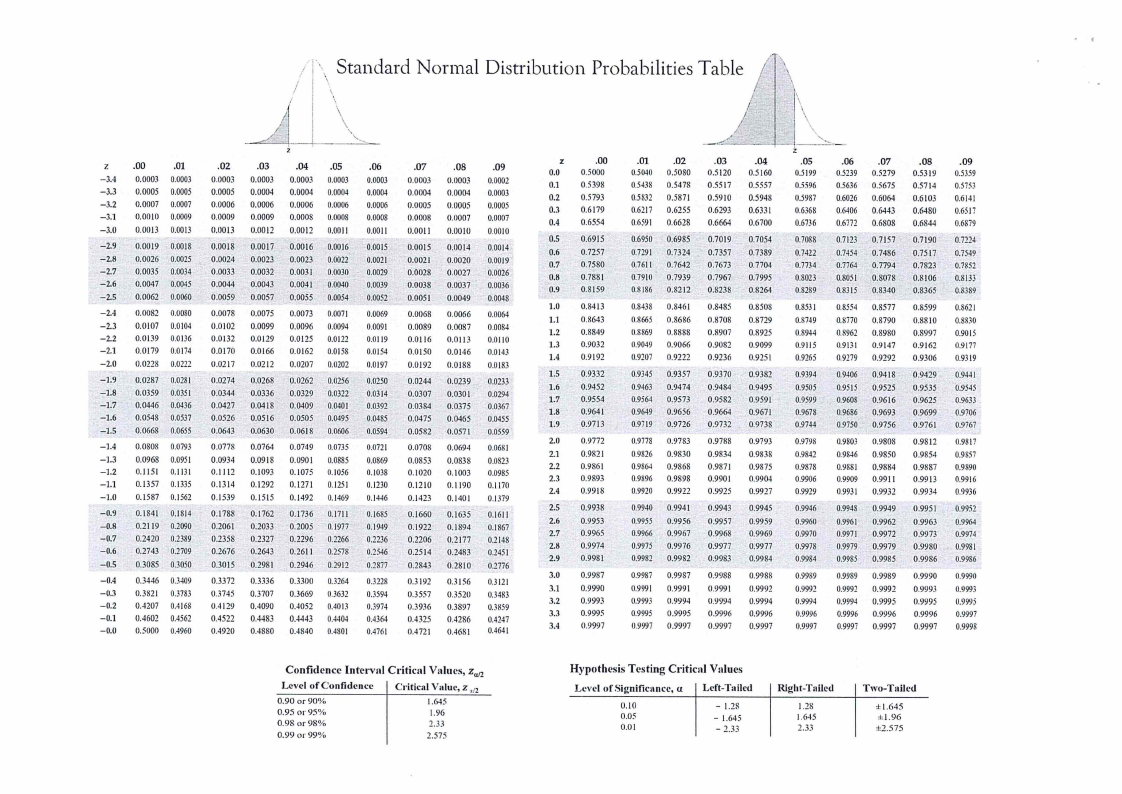
1. Normal distribution table
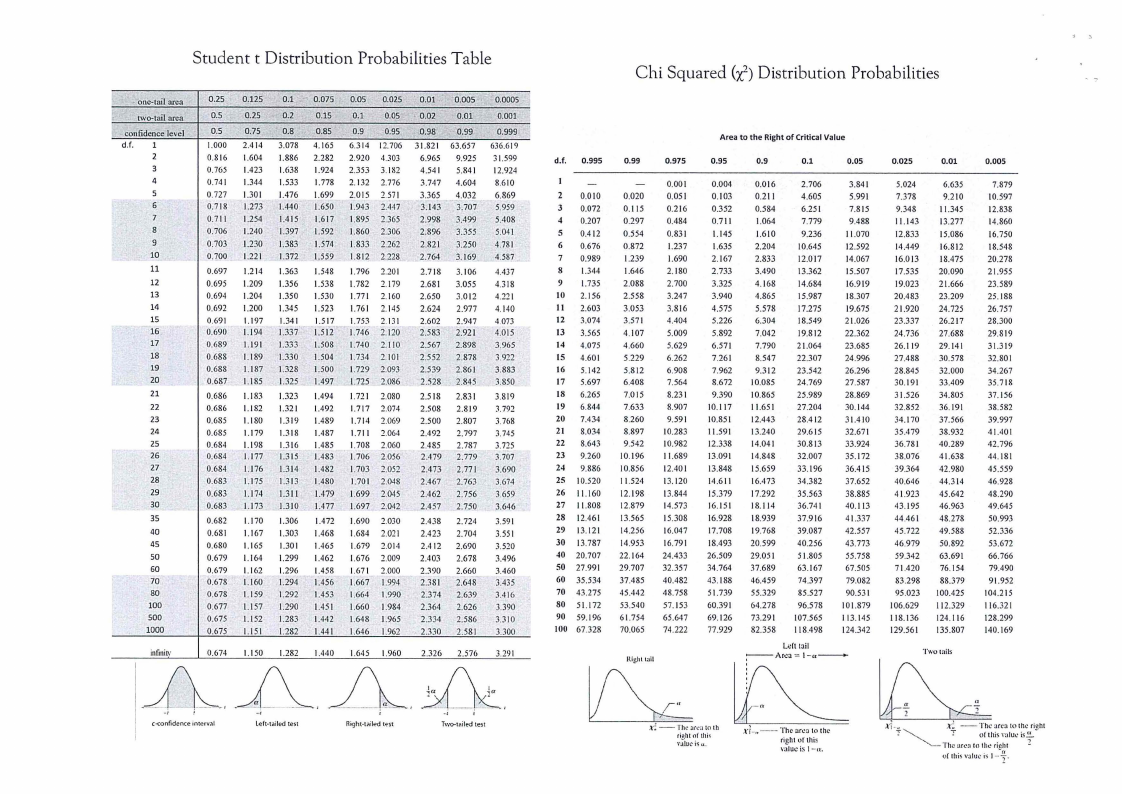
2. T-table
3. Chi-square table
THIS QUESTION PAPERCONSISTSOF 4 PAGES(Including this front page)
1
 |
2 Page 2 |
▲back to top |

Question 1 [25 marks]
1.1 Define the term survey methodology in your own words.
[3]
1.2 The Namibia Statistics Agency (NSA) is mandated to conduct annual Labour Force Surveys
(NLFS).Describe the basic characteristics of the NLFSin terms of the following:
1.2.1 one of the main objectives of the NLFS
1.2.2 the target population they try to describe
1.2.3 the sources from which they draw samples
1.2.4 the design of the way they sample people
1.2.5 the use of interviewers
1.2.6 the mode of data collection
1.2.7 the use of computers in the collection of responses
[7]
1.3 Define the following terms:
1.3.1 A random variable
[1]
1.3.2 Sampling unit
[1]
1.3.3 Population parameter
[1]
1.3.4 Random Sample
[1]
1.3.5 Statistical modeling
[1]
1.4 Provide a diagrammatically representation of a survey lifecycle from a quality perspective. [10]
Question 2 [25 marks]
2.1 Provide and explain four basic criteria for the acceptability of a sampling method?
[8]
2.2 Write at least 4 properties of the normal probability distribution
[4]
2.3 Write a short note on the importance of the normal distribution in sampling theory
[3]
2.4 The Ministry of Health and Social Services wants to estimate the rate of incidence of
respiratory disorders among the middle aged male and female smokers in Namibia. How large a
sample should be taken to be 95% confident that the error of estimation of the proportion of the
population with such disorders does not exceed 0.05? The true value of p is expected to be near
0.20.
[4]
2.5 To estimate the percentage of rats that carries a viral infection which produces a certain
sickness, 128 rats are examined and 72 of them are found to be infected. Calculate the standard
error of the estimated proportion and compute a 95% confidence interval for the population
proportion?
[6]
Question 3 [25 marks]
3.1 Distinguish between probability and non-probability sampling in terms of approaches to
sampling.
[4]
2
 |
3 Page 3 |
▲back to top |

3.2 Consider the population of 32 housing units organised into 8 clusters of 4 housing units in
each cluster. A sample of 3 clusters 2, 4, 8 was selected (n = 3) and all housing units within these 3
clusters were interviewed. The sample data collected are as follows.
Y21= 9
Y41= 6
Ys1= 10
Y22 =7
Y42= 5
Ys2= 11
Y23 =6
Y43= 8
Ys3 =3
Y24= 4
Y44 =9
Ys4 =8
Y2 =26
Y4 =28
Ys =32
3.2.1 Estimate Y, population total
[4]
3.2.2 Estimate y, average cluster value of the characteristic
[3]
3.2.3 Calculate Var(Y)
[4]
3.3 Recent census data on the number of cattle per farm are given below: Farms have been
stratified based on their total acreage (L=5). The present total number of farms in each stratum is
also given in the table.
For a sample of n = 500 farms, compute the sample sizes in each stratum under;
3.3.1 Proportional allocation
[5]
3.3.2 Optimal allocation
[5]
Stratum
h
I
II
Ill
IV
V
All strata
size
0-15
16-30
31-50
51-75
76 -100
Previous census
Total
Average
number of
number of
farms
N'h
cattle
Y- 1,
625
3.91
564
10.38
476
14.72
304
21.99
86
27.38
2055
Estimated
SD per
unit
I
S1,
4.5
7.3
9.6
12.2
15.8
Present total
number of
farms
Estimated
cost per
unit
~1
635
570
475
303
89
2072
Ch
3.50
2.75
2.25
3.00
2.50
Question 4 [25 marks]
4.1 Coding is a process in which questionnaire entries are assigned numeric values. The objective is
to prepare the data in a form suitable for entry into a computer. Provide three alternatives that the
coding operation may involve.
[6]
4.2 You have been approached by a client, Namibia Statistics Agency (NSA)to process the LFS2012
data and are required to estimate the number of working days you will take to enter 10, 000
questionnaires. The following information is provided:
a. 12 x data entry stations
b. 2 x shifts of data entry operators
 |
4 Page 4 |
▲back to top |
C. 7 x productive hours per work
d. 12 x operators
e. Average of 8,000 strokes per hour
f. 10,000 questionnaires
g. 2,500 strokes per questionnaires
h. 100 percent verification
[9]
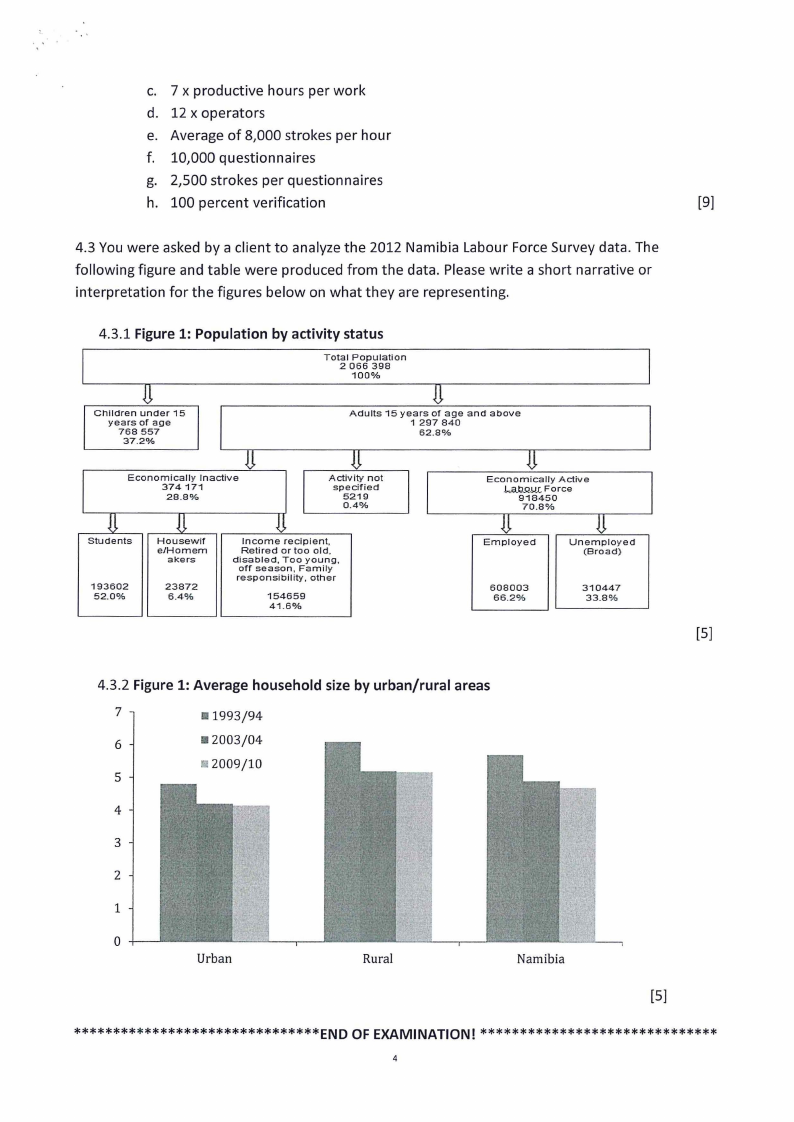
4.3 You were asked by a client to analyze the 2012 Namibia Labour Force Survey data. The
following figure and table were produced from the data. Please write a short narrative or
interpretation for the figures below on what they are representing.
4.3.1 Figure 1: Population by activity status
u
Total Population
2 066 398
100%
u
Children under 15
years of age
768 557
37.2%
Adults
15 years of age
1 297 840
62.8%
il
JJ
Economically
Inactive
374171
28.8%
Activity not
specified
5219
0.4%
H il
Students
193602
52.0%
Housewif
e/Homem
akers
23872
6.4%
Income recipient,
Retired or too old.
disabled, Too young,
off season, Family
responsibility,
other
154659
41.6%
and above
JJ
Economically Active
J.....<1.b..O-FUo.rl ce
918450
70.8%
JJ
JJ
Employed
Unemployed
(Broad)
608003
66.2%
310447
33.8%
[5]
4.3.2 Figure 1: Average household size by urban/rural areas
7
1993/94
6
2003/04
B 2009/10
5
4
3
2
1
0
Urban
Rural
Namibia
[SJ
*******************************END OFEXAMINATION**! ****************************
4
 |
5 Page 5 |
▲back to top |
/
I
I
, Standard Normal Distribution Probabilities Table
\\
'\\
' ·,__
·,._
z
.00
,01
.02
.03
.04 .05
.06
.07
.08
.09
-3.4 0.0003 0.0003 0.0003 0.0003 0.0003 0.0003 0.0003 0.0003 0.0003 0.0002
-3.3 0.0005 0.0005 0.0005 0.0004 0.0004 0.0004 0.0004 0.0004 0.0004 0.0003
-3.2 0.0007 0.0007 0.0006 0.0006 0.0006 0.0006 0.0006 0.0005 0.0005 0.0005
-3.1 0.0010 0.0009 0.0009 0.0009 0.0008 0.0008 0.0008 0.0008 0.0007 0.0007
-3.0 0.0013 0.0013 0.0013 0.0012 0.0012 0.001I 0.0011 0.0011 0.0010 0.0010
-2.9 0.0019 0.0018 0.0018 0.0017 0.0016 0.0016 0.0015 0.0015 0.0014 0.0014
-2.8 0.0026 0.0025 0.0024 0.0023 0.0023 0.0022 0.0021 0.0021 0.0020 0.0019
-2.7 0.0035 0.0034 0.0033 0.0032 0.0031 0.0030 0.0029 0.0028 0.0027 0.0026
-2.6 0.0047 0.0045 0.0044 0.0043 0.0041 0.0040 0.0039 0.0038 0.0037 0.0036
-2.5 0.0062 0.0060 0.0059 0.0057 0.0055 0.0054 0.0052 0.0051 0.0049 0.0048
-2.4 0.0082 0.0080 0.0078 0.0075 0.0073 0.0071 0.0069 0.0068 0.0066 0.0064
-2.3 0.0107 0.0104 0.0102 0.0099 0.0096 0.0094 0.0091 0.0089 0.0087 0.0084
-2.2 0.0139 0.0136 0.0132 0.0129 0.0125 0.0122 0.0119 0.0116 0.0113 0.0110
-2.1 0.0179 0.0174 0.0170 0.0166 0.0162 0.0158 0.0154 0.0150 0.0146 0.0143
-2.0 0.0228 0.0212 0.0217 0.0212 0.0207 0.0202 0.0197 0.0192 0.0188 0.0183
-1.9 0.0287 0.0281 0.0274 0.0268 0.0262 0.0256 0.0250 0.0244 0.0239 0.0233
-1.8 0.0359 0.0351 0.0344 0.0336 0.0329 0.0322 0.0314 0.0307 0.0301 0.0294
-1.7 0.0446 0.0436 0.0427 0.0418 0.0409 0.0401 0.0392 0.0384 0.0375 0.0367
-1.6 0.0548 0.0537 0.0526 0.0516 0.0505 0.0495 0.048S 0.0475 0.0465 0.0455
-1.5 0.0668 0.0655 0.0643 0.0630 0.0618 0.0606 0.0594 0.0582 0.0571 0.0559
-1.4 0.0808 0.0793 0.077S 0.0764 0.0749 0.0735 0.0721 0.0708 0.0694 0.0681
-1.3 0.0968 0.095I 0.0934 0.0918 0.0901 0.0885 0.0869 0.0853 0.0838 0.0823
-1.2 0.1151 0.1131 0.1112 O.l093 0. l075 0.1056 0.1038 0.1020 o.1003 0.0985
-1.1 0.1357 0.1335 0.1314 0.1292 0.1271 0.1251 0.1230 0.12IO 0.1190 0.1170
-1.0 0.1587 0.1562 0.1539 0.1515 0.1492 0.1469 0.1446 0.1423 0.1401 0.1379
-0.9 0.1841 0.1814 0.1788 0.1762 0.1736 0.1711 0.1685 0.1660 0.1635 0.1611
-0.8 0.2119 0.2090 0.2061 0.2033 0.2005 0.1977 0.1949 0.1922 0.1894 0.1867
-0.7 0.2420 0.2389 0.2358 0.2327 0.2296 0.2266 0.2236 0.2206 0.2177 0.2148
-0.6 0.2743 0.2709 0.2676 0.2643 0.2611 0.2578 0.2546 0.2514 0.2483 0.2451
-0.5 0.3085 0.3050 0.3015 0.2981 0.2946 0.2912 0.2877 0.2843 0.2810 0.2776
-0.4 0.3446 0.3409 0.3372 0.3336 0.3300 0.3264 0.3228 0.3192 0.3156 0.3121
-0.3 0.3821 0.3783 0..1745 0.3707 0.3669 0.3632 0.3594 0.3557 0.3520 0.3483
-0.2 0.4207 0.4168 0.4129 0.4090 0.4052 0.4013 0.3974 0.3936 0.3897 0.3859
-0.1 0.4602 0.4562 0.4522 0.4483 0.4443 0.4404 0.4364 0.4325 0.4286 0.4247
-0.0 0.5000 0.4960 0.4920 0.4880 0.4840 0.4801 0.4761 0.4721 0.4681 0.4641
z .oo
0.0 0.5000
0.1 0.5398
0.2 0.5793
0.3 0.6179
0.4 0.6554
.01
0.5040
0.5438
0.5832
0.6217
0.6591
.02
0.5080
0.5478
0.5871
0.6255
0.6628
.03
0.5120
0.5517
0.5910
0.6293
0.6664
.04
0.5160
0.5557
0.5948
0.6331
0.6700
z
.05
0.5199
0.5596
0.5987
0.6368
0.6736
.06
0.5239
0.5636
0.6026
0.6406
0.6772
.07
0.5279
0.5675
0.6064
0.6443
0.6808
.08
0.5319
0.5714
0.6103
0.6480
0.6844
.09
0.5359
0.5753
0.6141
0.651i
0.6879
0.5 0.6915
0.6 0.7257
0.7 0.7580
0.8 0.7881
0.9 0.8159
0.6950
0.7291
0.761I
0.7910
0.8186
0.6985
0.7324
0.7642
0.7939
0.8212
0.7019
0.7357
0.7673
0.7967
0.8238
0.7054
0.7389
0.7704
0.7995
0.8264
0.7088
0.7422
0.7734
0.8023
0.8289
0.7123
0.7454
0.7764
0.8051
0.8315
0.7157
0.7486
0.7794
0.8078
0.8340
0.7190
0.7517
0.7823
0.8106
0.8365
0.7224
0.7549
0.7852
0.8133
0.8389
1.0 0.8413
1.1 0.8643
1.2 0.8849
1.3 0.9032
1.4 0.9192
0.8438
0.8665
0.8869
0.9049
0.9207
0.8461
0.8686
0.8888
0.9066
0.9222
0.8485
0.8708
0.8907
0.9082
0.9236
0.8508
0.8729
0.8925
0.9099
0.9251
0.8531
0.8749
0.8944
0.9115
0.9265
0.8554
0.8770
0.8962
0.9131
0.9179
0.8577
0.8790
0.8980
0.9147
0.9292
0.8599
0.8810
0.8997
0.9162
0.9306
0.8621
0.8830
0.9015
0.9177
0.9319
1.5 0.9332
1.6 0.9452
1.7 0.9554
1.8 0.9641
1.9 0.9713
0.9345
0.9463
0.9564
0.9649
0.9719
0.9357
0.9474
0.9573
0.9656
0.9726
0.9370
0.9484
0.9582
0.9664
0.9732
0.9382
0.9495
0.9591
0.9671
0.9738
0.9394
0.9505
0.9599
0.9678
0.9744
0.9406
0.9515
0.9608
0.9686
0.9750
0.9418
0.9525
0.9616
0.9693
0.9756
0.9429
0.9535
0.9625
0.9699
0.9761
0.9441
0.9545
0.9633
0.9706
0.9767
2.0 0.9772
2.1 0.9821
2.2 0.9861
2.3 0.9893
2.4 0.9918
0.9778
0.9826
0.9864
0.9896
0.9920
0.9783
0.9830
0.9868
0.9898
0.9922
0.9788
0.9834
0.9871
0.9901
0.9925
0.9793
0.9838
0.9875
0.9904
0.9927
0.9798
0.9842
0.9878
0.9906
0.9929
0.9803
0.9846
0.9881
0.9909
0.9931
0.9808
0.9850
0.9884
0.991I
0.9932
0.9812
0.9854
0.9887
0.9913
0.9934
0.9817
0.9S57
0.9890
0.9916
0.9936
2.5 0.9938
2.6 0.9953
2.7 0.9965
2.8 0.9974
2.9 0.9981
0.9940
0.9955
0.9966
0.9975
0.9982
0.9941
0.9956
0.9967
0.9976
0.9982
0.9943
0.9957
0.9968
0.9977
0.9983
0.9945
0.9959
0.9969
0.9977
0.9984
0.9946
0.9960
0.9970
0.9978
0.9984
0.9948
0.9961
0.9971
0.9979
0.9985
0.9949
0.9962
0.9972
0.9979
0.9985
0.9951
0.9963
0.9973
0.9980
0.9986
0.9952
0.9964
0.9974
0.9981
0.9986
3.0 0.9987
3.1 0.9990
3.2 0.9993
3.3 0.9995
3.4 0.9997
0.9987
0.9991
0.9993
0.9995
0.9997
0.9987
0.9991
0.9994
0.9995
0.9997
0.9988
0.9991
0.9994
0.9996
0.9997
0.9988
0.9992
0.9994
0.9996
0.9997
0.99S9
0.9992
0.9994
0.9996
0.9997
0.9989
0.9992
0.9994
0.9996
0.9997
0.9989
0.9992
0.9995
0.9996
0.9997
0.9990
0.9993
0.9995
0.9996
0.9997
0.9990
0.9993
0.9995
0.9997
0.9998
Confidence Interval Cdtical Values, Zun.
Level of Confidence
0.90 or90%
0.95 or 95%
0.98 or98%
0.99 or99%
Critical Value, z •12
1.645
1.96
2.33
2.575
Hypothesis Testing Critical Values
Level of Significnncc, u Left-Tailed
0.10
- 1.28
0.05
- 1.645
0.01
- 1.33
Right-Tailed
1.28
1.645
2.33
Two-Tailed
±1.645
±1.96
±2.575
 |
6 Page 6 |
▲back to top |
Student t Distribution Probabilities Table
I - one-tail area
two-tail nrea
I confidence level
d.f. 1
2
3
4
5-
I
6
7
'I
8
'I
'
-
9
10
11
12
13
14
- . -
15
16
I
17
I
18
19
L_
20
21
22
23
24
25
26
27
28
29
-
30
,.
35
40
45
50
-
60
-
70
80
100
500
1000
0.25
0.5
0.5
1.000
0.816
0.765
0.741
0.727
0.718
0.711
0.706
0.703
0.700
0.697
0.695
0.694
0.692
0.691
0.690
0.689
0.688
0.688
0.687
0.686
0.686
0.685
0.685
0.684
0.684
0.684
0.683
0.683
0.683
0.682
0.681
0.680
0.679
0.679
0.678
0.678
0.677
0.675
0.675
0.125
0.25
0.75
2.414
1.604
1.423
1.344
1.301
1.273
1.254
1.240
1.230
1.221
1.214
1.209
1.204
1.200
1.197
1.194
1.191
1.189
1.187
1.185
1.183
1.182
1.180
1.179
1.198
1.177
1.176
1.175
1.174
1.173
1.170
1.167
I. 165
1.164
1.162
1.160
1.159
1.157
1.152
1.151
0.1
0.2
0.8
3.078
1.886
1.638
1.533
1.476
1.440
1.415
1.397
1.383
1.372
1.363
1.356
1.350
1.345
1.341
1.337
1.333
1.330
1.328
1.325
1.323
1.321
1.319
1.318
1.316
1.315
1.314
1.313
1.311
1.319
1.306
1.303
1.301
1.299
1.296
1.294
1.292
1.290
1.283
1.282
0.075
0.15
0.85
4.165
2.282
1.924
1.778
1.699
1.650
1.617
1.592
1.574
1.559
1.548
1.538
1.530
1.523
1.517
1.512
1.508
1.504
1.500
1.497
1.494
1.492
1.489
1.487
1.485
1.483
1.482
1.480
1.479
1.477
1.472
1.468
1.465
1.462
1.458
1.456
1.453
1.451
1.442
1.441
0.05
0.1
0.9
6.314
2.920
2.353
2.132
2.015
1.943
1.895
1.860
1.833
1.812
1.796
1.782
1.771
1.761
1.753
1.746
1.740
1.734
1.729
1.725
1.721
1.717
1.714
1.711
1.708
1.706
1.703
1.701
1.699
1.697
1.690
1.684
1.679
1.676
1.671
1.667
1.664
1.660
1.648
1.646
0.025
a.as
0.95
12.706
4.303
3. 182
2.776
2.571
2.447
2.365
2.306
2.262
2.228
2.201
2.179
2.160
2.145
2.131
2.120
2.110
2.101
2.093
2.086
2.080
2.074
2.069
2.064
2.060
2.056
2.052
2.048
2.045
2.042
2.030
2.021
2.014
2.009
2.000
1.994
1.990
1.984
1.965
1.962
0.01
0.02
0.98
31.821
6.965
4.541
3.747
3.365
3.143
2.998
2.896
2.821
2.764
2.718
2.681
2.650
2.624
2.602
2.583
2.567
2.552
2.539
2.528
2.518
2.508
2.500
2.492
2.485
2.479
2.473
2.467
2.462
2.457
2.438
2.423
2.412
2.403
2.390
2.381
2.374
2.364
2.334
2.330
0.005
0.01
0.99
63.657
9.925
5.841
4.604
4.032
3,707
3.499
3.355
3.250
3.169
3.106
3.055
3.012
2.977
2.947
2.921
2.898
2.878
2.861
2.845
2.831
2.819
2.807
2.797
2.787
2.779
2.771
2.763
2.756
2.750
2.724
2.704
2.690
2.678
2.660
2.648
2.639
2.626
2.586
2.58]
0.0005
0.001
0.999
636.619
31.599
12.924
8.610
6.869
5.959
5.408
5.041
4.781
4.587
4.437
4.318
4.221
4.140
4.073
4.015
3.965
3.922
3.883
3.850
3.819
3.792
3.768
3.745
3.725
3.707
3.690
3,674
3.659
3.646
3.591
3.551
3.520
3.496
3.460
3.435
3.416
3.390
3.310
3.300
inlinitY
0.674 I. ISO 1.282 1.440 1.645 1.960
A.A.Lk~. M,
t
-r
1
C<onfidenceintervttl
LefMailedtest
Right•t.liledtest
2.326 2.576 3.291
•. ,
,
Two-tailedtest
Chi Squared (x2) Distribution Probabilities
d.f. 0.995
0.99
0.975
2 0.010
3 0.072
4 0.207
5 0.412
6 0.676
7 0.989
8 1.344
9 1.735
10 2.156
11 2.603
12 3.074
13 3.565
14 4.075
15 4,601
16 5.142
17 5.697
18 6.265
19 6.844
20 7.434
21 8.034
22 8.643
23 9.260
24 9.886
25 10.520
26 11.160
27 11.808
28 12.461
29 13.121
30 13.787
40 20.707
50 27.991
60 35.534
70 43.275
80 51.172
90 59.196
100 67.328
0.020
0.1 IS
0.297
0.554
0.872
1.239
1.646
2.088
2.558
3.053
3.571
4.107
4.660
5.229
5.812
6.408
7.015
7.633
8.260
8.897
9.542
10.196
10.856
11.524
12.198
12.879
13.565
14.256
14.953
22.164
29.707
37.485
45.442
53.540
61.754
70.065
0.001
0.051
0.216
0.484
0.831
1.237
1.690
2.180
2.700
3.247
3,816
4.404
5.009
5.629
6.262
6.908
7.564
8.231
8.907
9.591
10.283
10.982
11.689
12.401
13.120
13.844
14.573
15.308
16.047
16.791
24.433
32.357
40.482
48.758
57.153
65.647
74.222
Right 1:.1il
Area to the Right of Critical Value
0.95
0.9
0.1
0.05
0.004
0.103
0.352
0.711
1.145
1.635
2.167
2.733
3.325
3.940
4.575
5.226
5.892
6.571
7.261
7.962
8.672
9,390
10.117
10.851
11.591
12.338
13.091
13.848
14.611
15.379
16.151
16.928
17.708
18.493
26.509
34.764
43.188
51.739
60.391
69.126
77.929
0.016
0.21 I
0.584
1.064
1.610
2.204
2.833
3.490
4.168
4.865
5.578
6.304
7.042
7.790
8.547
9.312
I0.085
10.865
11.651
12.443
13.240
14.041
14.848
15.659
16.473
17.292
18.114
18.939
19.768
20.599
29.051
37,689
46.459
55.329
64.278
73.291
82.358
2.706
4.605
6.251
7.779
9.236
10.645
12.017
13.362
14.684
15.987
17.275
18.549
19.812
21.064
22.307
23.542
24.769
25.989
27.204
28.412
29.615
30.813
32.007
33,196
34.382
35.563
36.741
37.916
39.087
40.256
51.805
63.167
74.397
85.527
96.578
107.565
118.498
Lerttail
~Arca=t-u-
3.841
5.991
7.815
9.488
11.070
12.592
14.067
15.507
16.919
18.307
19.675
21.026
22.362
23.685
24.996
26.296
27.587
28.869
30.144
31.410
32.671
33.924
35.172
36.41 S
37.652
38.885
40.113
41.337
42.557
43,773
55. 758
67.505
79.082
90,531
101.879
113.145
124.342
0.025
0.01
5,024
7,378
9,348
11.143
12.833
14.449
16.013
I 7.535
19.023
20.483
21.920
23,337
24.736
26.119
27.488
28.845
30.191
31.526
32.852
34.170
35.4 79
36.781
38.076
39.364
40.646
41.923
43.195
44.461
45.722
46.979
59.342
71.420
83.298
95.023
106.629
118.136
129.561
6,635
9.210
11.345
13.277
15.086
16.812
18.475
20.090
21.666
23.209
24.725
26.217
27.688
29.141
30.578
32.000
33.409
34.805
36.191
37.566
38.932
40.289
41.638
42.980
44.314
45.642
46.963
48.278
49.588
50.892
63.691
76.154
88.379
I 00.425
112.329
124.116
135.807
Two13iJs
0.005
7.879
10.597
12.838
14.860
16.750
18.548
20.278
21.955
23.589
25. 188
26.757
28.300
29.819
31.319
32.801
34.267
35.718
37.156
38.582
39.997
41.401
42.796
44.181
45.559
46.928
48.290
49.645
50.993
52.336
53.672
66.766
79.490
91.952
104.215
116.321
128.299
140. 169
.,.,: -
n1,·a,~·ato lh
ri£1,hnlf thi~
\\'~IUl' is u.
--
xi-..··---T·h-e ar\\!ato rhc
rightof this
valu..:is I-tr.
--,?.i.,
x~ -Th..:
:m::1to the ri!'.!,ht
T
ofthisvalu1.•is~~
--~f. --The arc:1IO !he ri~hl
2
of !his v::ilu~i-;I





