 |
NUM701S - NUMERICAL METHODS - 1ST OPP - JUNE 2023 |
 |
1 Page 1 |
▲back to top |

nAmlBIA unlVERSITY
OF SCIEnCE Ano TECHnOLOGY
FACULTYOF HEALTH,NATURALRESOURCESAND APPLIEDSCIENCES
SCHOOLOF NATURALAND APPLIEDSCIENCES
DEPARTMENT OF MATHEMATICS, STATISTICS AND ACTUARIAL SCIENCE
QUALIFICATION:
BACHELOROF SCIENCEIN APPLIEDMATHEMATICSAND STATISTICS
QUALIFICATION CODE: 07BSAM
LEVEL: 7
COURSE CODE: NUM701S
COURSE NAME: NUMERICAL METHODS 1
SESSION:
DURATION:
JUNE 2023
3 HOURS
PAPER: THEORY
MARKS: 100
EXAMINERS
FIRSTOPPORTUNITY EXAMINATION QUESTION PAPER
Dr S. N. NEOSSINGUETCHUEAND G. S. MBOKOMA
MODERATOR:
Prof S. S. MOTSA
INSTRUCTIONS
1. Answer ALL the questions in the booklet provided.
2. Show clearly all the steps used in the calculations. All numerical results must be
given using 4 decimals where necessary unless mentioned otherwise.
3. All written work must be done in blue or black ink and sketches must be done in
pencil.
PERMISSIBLEMATERIALS
1. Non-programmable calculator without a cover.
THIS QUESTION PAPER CONSISTS OF 3 PAGES (Including this front page)
Attachments
None
 |
2 Page 2 |
▲back to top |

Problem 1 [28 marks]
1-1. Write down the general formula of the Taylor's expansion with the Lagrange and the the
integral remainder term respectively of a function f (x) about a point x = x0 .
[6]
1-2. We want to generate the Taylor series of f(x) = sin(x) about x0 = 0 in summation form.
1-2-1 Compute f' and f" and show by induction on k E N that
[5]
1-2-2 Deduce the expression of the Taylor series of f(x) = sin(x) about x0 = 0.
[5]
1-3. Suppose that g : [a,b] --+ [a,b]is continuous on the real interval [a,b] and is a contraction
in the sense that there exists a constant ,\\ E (0, 1) such that
lg(x) - g(y)I :S>-Ix- YI,for all x, y E [a,b].
Prove that there exists a unique fixed point in [a,b] and that the fixed point iteration Xn+1 =
g(xn) converges to it for any x0 E [a,b]. Also, prove that the error is reduced by a factor of at
least >.from each iteration to the next.
[12]
Problem 2. [45 marks]
2-1. Write down in details the formulae of the Lagrange and Newton's form of the polynomial
that interpolates the set of data points (xo, f(xo)), (x 1, f(xi)), ... , (xn, f(xn)).
[7]
2-2. Use the results in 2-1. to determine the Lagrange and Newton's form of the polynomial
that interpolates the set of data points (1, 1), (2, 5) and (3, 15).
[18]
2-3. Determine the error term for the formula
[15]
J"'(x) 2h13 [3f(x + h) - lOf(x) + 12f(x - h) - 6f(x - 2h) + f(x - 3h)]
2-4. State the central difference formula to approximate f"(x 0) and use it to approximate
f"(0.5) when f(x) = ln(l + x) and h = 0.001.
[5]
Problem 3. [27 marks]
The fourth-order Runge-Kutta (RK4) method to solve the IVP y'(t) = f(t, y), y(to) = Yousing
n steps is described by the following algorithm
Given f, to, Yo,t1, n, let h = (t1 - to)/n
For k = 0, 1, ... , n - 1
Kl = f(tk, Yk)
K2 = f(tk + ~'Yk + ~Kl)
K3 = f(tk + 2' Yk + 2K2)
K4 = f(tk + h, Yk + hK3)
Yk+l= Yk + (h/6)[Kl + 2K2 + 2K3 + K4]
tk+l = tk + h
End For
3-1. Write down the RK4 algorithm for the following specific problem after n steps
[7]
y' (t) = y - t2 + 1, y (0) = 2
1
 |
3 Page 3 |
▲back to top |
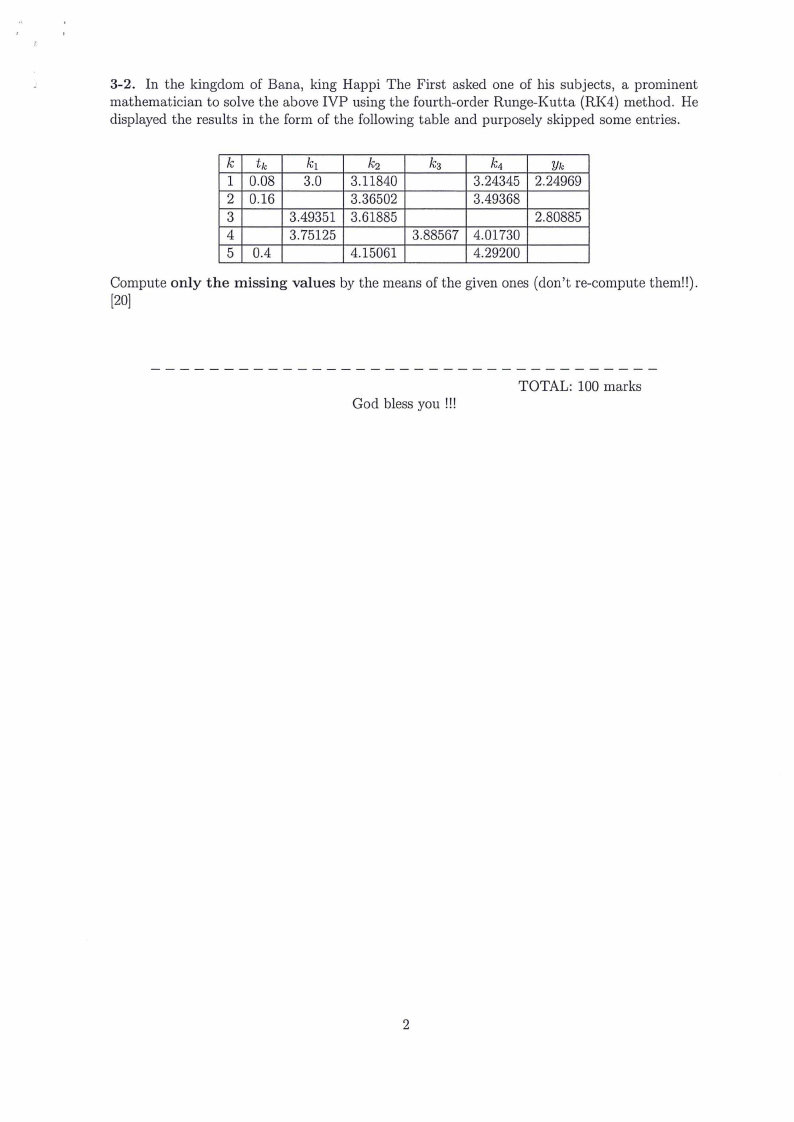
3-2. In the kingdom of Bana, king Happi The First asked one of his subjects, a prominent
mathematician to solve the above IVP using the fourth-order Runge-Kutta (RK4) method. He
displayed the results in the form of the following table and purposely skipped some entries.
k tk
k1
k2
k3
k4
Yk
1 0.08 3.0 3.11840
3.24345 2.24969
2 0.16
3.36502
3.49368
3
3.49351 3.61885
2.80885
4
3.75125
3.88567 4.01730
5 0.4
4.15061
4.29200
Compute only the missing values by the means of the given ones (don't re-compute them!!).
[20]
Goel bless you !!!
TOTAL: 100 marks
2





