 |
ARI711S - ARTIFICIAL INTELLIGENCE - 2ND OPP - JULY 2024 |
 |
1 Page 1 |
▲back to top |

I
nAmlBIA
UntVERSITY
OF SCIEnCE
Ano TECHnOLOGY
FACULTY OF COMPUTING AND INFORMATICS
DEPARTMENT OF SOFTWARE ENGINEERING
QUALIFICATION: BACHELOROF COMPUTER SCIENCE(SOFTWARE DEVELOPMENT)
QUALIFICATION CODE: 07BACS
LEVEL:7
COURSE:ARTIFICIAL INTELLIGENCE
COURSECODE: ARl711S
DATE: JULY 2024
SESSION:THEORY
DURATION: 3 HOURS
MARKS: 100
SECONDOPPORTUNITY\\ SUPPLEMENTARYEXAMINATION QUESTIONPAPER
EXAMINER:
MR ISAAC MAl<OSA & MR IMMANUEL l<ANDJABANGA
MODERATOR
MS PAULINA SHIFUGULA
THIS QUESTION PAPERCONSISTSOF 7 PAGES
(Including this front page)
INSTRUCTIONSTO STUDENTS:
1. Read all the questions, passages, scenarios, etc., carefully before answering.
2. All questions must be answered in the Answer Booklet. Clearly indicate the question number
for each answer.
3. Please, ensure that your writing is legible, neat and presentable.
4. There are no books, notes or any other additional aids allowed in the examination.
5. Use the allocated marks as a guideline when answering questions.
6. Looking at other students' work is strictly prohibited.
PERMISSIBLEMATERIALS
1. Calculator
2. Ruler
1
 |
2 Page 2 |
▲back to top |

I
Question 1 -True or false
(16 marks)
Select whether the following statements are either TRUE or FALSE.(2 marks each)
1.1. Depth-First Search (DFS)is always the best choice for finding all possible solutions in a
search problem.
1.2. MDPs are a powerful tool for modelling and solving decision-making problems in
various domains like robotics, game playing, and resource allocation.
1.3. In an MDP, the agent has complete knowledge of the entire state of the environment at
any given time.
1.4. A CSPinvolves assigning values to variables such that all the constraints between them
are satisfied.
1.5. Breadth-First Search (BFS)is guaranteed to find the shortest path between two points in
a graph.
1.6. CSPsare only applicable to problems with numerical variables.
1.7. Heuristic functions are used to evaluate the potential cost of reaching the goal state in a
search problem.
1.8. Alpha-Beta Pruning can be used to improve the efficiency of minimax search in two-
player zero-sum games.
Question 2
(2 marks)
How does using additional knowledge make informed search algorithms more efficient than
uninformed search algorithms?
Question 3
(4 marks)
Discussthe trade-offs between using a simple reflex agent and a model-based agent in an
intelligent vacuum cleaner. Consider factors like efficiency, adaptability, and robustness in
your answer.
2
 |
3 Page 3 |
▲back to top |

Question 4
(6 marks)
In your own words, explain what a search problem entails. What are the key components
involved?
Question 5
(4 marks)
Considering the properties of search algorithms, which property would be most relevant to
add to the following description:
Property
Description
A measure of how much memory the algorithm needs to run.
A measure of how long it takes the algorithm to find a
solution (typically based on the number of steps involved).
A guarantee that the algorithm will find the solution with the
lowest cost among all possible solutions.
A guarantee that the algorithm will find a solution if one
exists.
Question 6 - Graph Search
(18 marks)
6.1. Consider the graph shown below where the numbers on the links are link costs and the
numbers next to the states are heuristic estimates. Note that the arcs are undirected. Let A
be the start state and G be the goal state.
3
4
9
D
1
3
 |
4 Page 4 |
▲back to top |
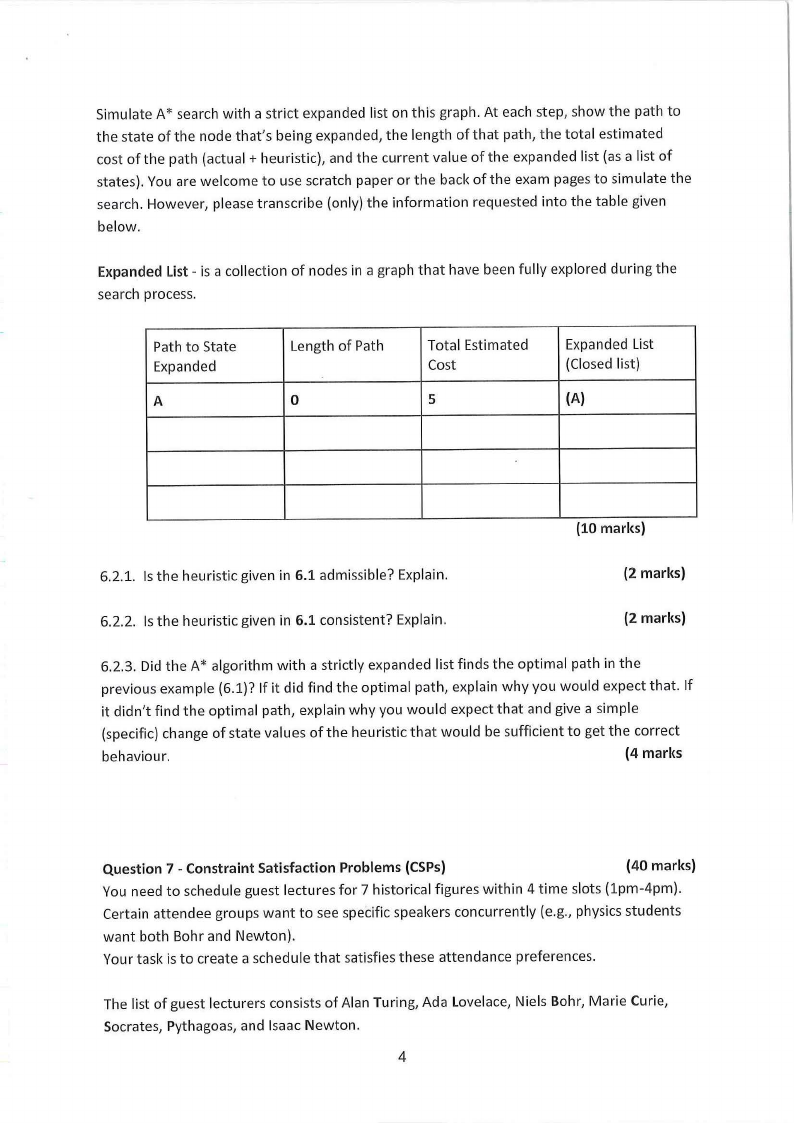
Simulate A* search with a strict expanded list on this graph. At each step, show the path to
the state of the node that's being expanded, the length of that path, the total estimated
cost ofthe path (actual+ heuristic), and the current value of the expanded list (as a list of
states). You are welcome to use scratch paper or the back of the exam pages to simulate the
search. However, please transcribe (only) the information requested into the table given
below.
Expanded List- is a collection of nodes in a graph that have been fully explored during the
search process.
Path to State
Expanded
A
Length of Path
0
Total Estimated
Cost
5
Expanded List
(Closed list)
(A)
(10 marks)
6.2.1. Is the heuristic given in 6.1 admissible? Explain.
(2 marks)
6.2.2. Is the heuristic given in 6.1 consistent? Explain.
(2 marks)
6.2.3. Did the A* algorithm with a strictly expanded list finds the optimal path in the
previous example (6.1)? If it did find the optimal path, explain why you would expect that. If
it didn't find the optimal path, explain why you would expect that and give a simple
(specific) change of state values of the heuristic that would be sufficient to get the correct
behaviour.
(4 marks
Question 7 - Constraint Satisfaction Problems (CSPs)
(40 marks)
You need to schedule guest lectures for 7 historical figures within 4 time slots {1pm-4pm).
Certain attendee groups want to see specific speakers concurrently (e.g., physics students
want both Bohr and Newton).
Your task is to create a schedule that satisfies these attendance preferences.
The list of guest lecturers consists of Alan Turing, Ada Lovelace, Niels Bohr, Marie Curie,
Socrates, Pythagoas, and Isaac Newton.
4
 |
5 Page 5 |
▲back to top |

• Turing has a scheduling constraint. He can only be assigned the 1pm time slot.
• The Course VIII students want to see the physicists: Bohr, Curie, and Newton.
• The Course XVIII students want to see the mathematicians: Lovelace, Pythagoras,
and Newton.
• The members of the Ancient Greece Club want to see the ancient Greeks: Socrates
and Pythagoras.
• The visiting Wellesley students want to see the female speakers: Lovelace and Curie.
• The CME students want to see the British speakers: Turing, Lovelace, and Newton.
• Finally, you decide that you will be happy if and only if you get to see both Curie and
Pythagoras. (Yes, even if you belong to one or more of the groups above.)
7.1. Draw a constraint graph using the initials of each pair of lecturers who cannot share a
time slot.
(6 marks)
Constraint graph for this problem
©
®
®
®
Domains for this problem
T
1
L
1,2,3,4
B
1,2,3,4
C
1,2,3,4
s
1,2,3,4
p
1,2,3,4
N
1,2,3,4
7.2. Search for a solution using backtracking only-without any forward checking or
propagation. The only check is to make sure that each new assignment violates no
constraint with any previous assignment. As a tiebreaker, assign a lecturer to the earliest
available time slot. Continue up to the first time you try and fail to assign any time to
5
 |
6 Page 6 |
▲back to top |
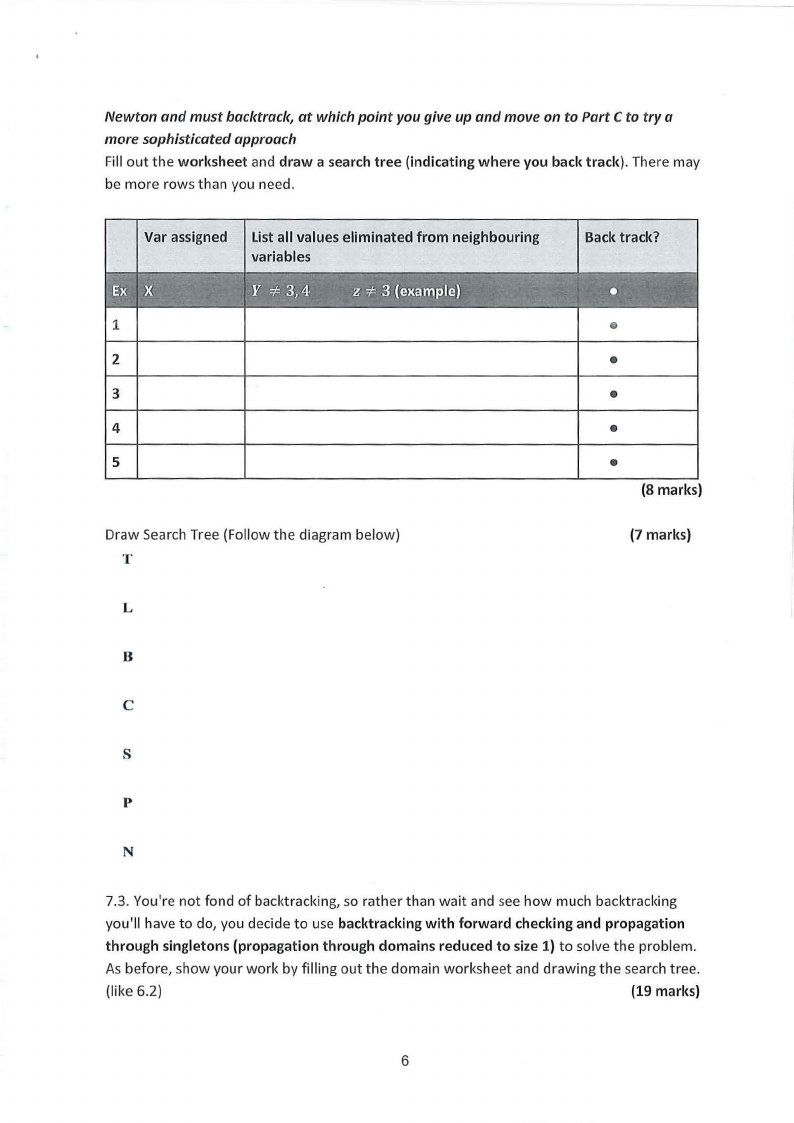
Newton and must baclctrack, at which point you give up and move on to Part C to try a
more sophisticated approach
Fill out the worksheet and draw a search tree (indicating where you back track). There may
be more rows than you need.
Var assigned List all values eliminated from neighbouring
variables
Back track?
1
2
3
4
5
Draw Search Tree (Follow the diagram below)
T
•
•
•
•
(8 marks)
(7 marks)
L
B
C
s
p
N
7.3. You're not fond of backtracking, so rather than wait and see how much backtracking
you'll have to do, you decide to use backtracking with forward checking and propagation
through singletons (propagation through domains reduced to size 1) to solve the problem.
As before, show your work by filling out the domain worksheet and drawing the search tree.
(like 6.2)
(19 marks)
6
 |
7 Page 7 |
▲back to top |

Question 8 - Markov Decision Processes (MDPs)
(10 marks)
Consider the MDP given in the figure below. Assume the discount factory= 0.9. The
r-values are rewards, while the numbers next to arrows are probabilities of outcomes. Note
that only state 51 has two actions. The other states have only one action for each state.
1.0
8.1. Write down the numerical value of J(S1) after the first and the second iterations of
Value Iteration?
(5 marks)
Initial value function:
.J0 (So) = O;J 0 (Si) = O;J0 (S2) = O; J0 (S3) = O;
.!1 (81) =
.J2 (S1)=
8.2. Write down the optimal value of state S1. There are few ways to solve it, and for one of
them you may find the following equality: P00 i=O a i = 11-a for any Os; a< 1. (5 marks)
- END OF QUESTION PAPER -
7





