 |
SAT802S - SAMPLING THEORY - 1ST OPP - NOV 2022 |
 |
1 Page 1 |
▲back to top |

nAm I Bl A un IVERSITY
OF SCIEnCE Ano TECHno LOGY
FACULTYOF HEALTHAND APPLIEDSCIENCES
DEPARTMENTOF MATHEMATICSAND STATISTICS
QUALIFICATION:BACHELOROF SCIENCEHONOURS IN APPLIEDSTATISTICS
QUALIFICATION CODE:
08BSHS
LEVEL: 8
COURSECODE: SAT802S
COURSE:SAMPLING THEORY
SESSION: November 2022
PAPER: THEORY
DURATION: 3 Hours
MARKS: 100
EXAMINER
MODERATOR:
FIRSTOPPORTUNITYEXAMINATION QUESTION PAPER
Mr. J. J. SWARTZ
Dr. I. NEEMA
INSTRUCTIONS
1. Answer ALL the questions in the booklet provided.
2. Show clearly all the steps used in the calculations.
3. All written work must be done in blue or black ink and sketches must be done in pencil.
PERMISSIBLEMATERIALS
1. Calculator
2. Pen and Clean Paper for calculations
THIS QUESTION PAPERCONSISTSOF 4 PAGES{Including this front page)
 |
2 Page 2 |
▲back to top |

Question 1 [25 marks]
1.1 Write a short description on the importance of the normal distribution in sampling
theory.
[4]
1.2 Provide six basic steps in developing a sampling plan.
[6]
1.3 For the 200 managers and 800 engineers of a corporation, the standard deviations of
the number of days a year spent on research were presumed to be 30 and 60 days,
respectively. Find the sample size needed for proportional allocation to estimate the
population mean with the S.E.of the estimator not exceeding 10 and its allocation for the
two groups.
[5]
1.4 Among 100 Retailers in Namibia, the average of employee sizes for the largest 10 and
smallest 10 corporations were known to be 300 and 100, respectively. For a sample of 20
from the remaining 80 retailers, the mean and standard deviation were 250 and 110,
respectively. For the total employee size of the 80 retailers, find the
1.4.1 Estimate for the total,
[2]
1.4.2 S.E.of the estimate, and
[3]
1.4.3 95% confidence limits.
[5]
Question 2 [25 marks]
2.1. The Ministry of Health and Social Services (MoHSS)wants to estimate the rate of
incidence of respiratory disorders among the middle-aged male and female smokers in
Namibia. How large a sample should be taken to be 95% confident that the error of
estimation of the proportion of the population with such disorders does not exceed 0.05?
The true value of p is expected to be near 0.30.
[5]
2.2.
We propose to estimate the mean Y of a characteristic y by way of a sample selected
according to a simple random design without replacement of size 1000 in a population of
size 1 000 000. We know the mean X = l 5 of an auxiliary characteristic x . We have
the following results:
,
')
,.:::,_
..:....
s .~ = 2 0 , s .; = 2 5 , s xy = I 5 , X = I 4 , Y = 1 0
2.2.1. Estimate Y by way of Horwitz - Thomson, difference, ratio and regression
estimators. Estimate the variances of these estimators.
[15]
2.2.2. Which estimator should we choose to estimate Y ?
[5]
Question 3 [25 marks]
3.1. The Namibian 25, 2001, summarized the results of a survey conducted by Yellow
Expresson 2000 lawyers on sexual advances in the office. Between 85 and 98% responded
to the questions in the survey; 49% of the responding women and 9% of the responding
men agreed that some sorts of harassment exist in the offices. Assume that the population
of lawyers is large and there are equal numbers of female and male lawyers, and ignore the
nonresponse; that is, consider the respondents to be a random sample of the 2000 lawyers.
3.1.1 Find the standard errors for the above percentages.
[5]
 |
3 Page 3 |
▲back to top |

3.2. A forest resource manager is interested in estimating the total number of dead trees in
a 400 acre area of heavy infestation. She subdivides the area into 200 plots of equal sizes
and uses photo counts to find the number of dead trees in 18 randomly sampled plots. She
then randomly samples 8 plots out of these 18 plots and conducts a ground count on these
8 plots. Let x denote the number of dead trees in the plot by photo count and y the number
of dead trees by ground count. The data are given as:
Plot
123
4 5 6 7 8 9 10 11 12 13 14 15 16 17 18
x'
5 7 10 6 7 9 3 6 8 11 5
9
12 13 3
20 15 4
Out of these 18 plots, 8 are randomly selected and a ground count is conducted.
Plot
2
X
7
y
9
y-rx
0.3375
3
10
13
0.6250
5
7
10
1.3375
6
9
11
-0.1375
12
9
10
-1.1375
15
3
4
0.2875
3.2.1 Estimate the total number of dead trees in the 400-acre area.
3.2.2 Compute the ratio estimate for the population total.
3.2.3 Compute the estimated variance of the ratio estimator
16
20
25
0.2500
17
15
17
-1.5625
[6]
[6]
[8]
Question 4 [25 marks]
4.1 A mathematics achievement test was given to 486 students prior to entering a certain
college who then took a calculus class. A simple random sampling of 10 students are
selected and their calculus score recorded. It is known that the average achievement test
score for the 486 students was 52. The scatterplot of the 10 samples are given below and
the data follow.
".'.',-_
..,_
>-
70 -
eo -
"°
:,0
30
"" "" CIO
ro
so
X
The scatter plot shows that there is a strong positive linear relationship.
µL= y + b(µ, - :r) = a+ bµ,
Student
I
2
3
4
5
6
7
8
9
Achin·ement test
scorcX
39
43
21
64
57
47
28
75
34
Calculus Jcore Y
65
78
52
82
92
89
73
98
56
!he re~ression equation is
1 = 4 .8 + .766 X
?redicto.r
Coe:f Si;;Dev
I
Constani: 4 .734 8.50
4.79
X
0.7€56
O.l SO
4.38
S,. 8. 04 R-Sq 70.S\\ 'R-Sq(adj)
p
0.0.l
o.o z
= 66.8-t
Jmaly.sis of Va::ian<:e
Source
OF SS
Regression
l 450.0
Resid. Err 8 606.0
Total
9 !056.0
M5
l~So.o
75.8
:
19.14
P
o.oo_
10
52
75
 |
4 Page 4 |
▲back to top |
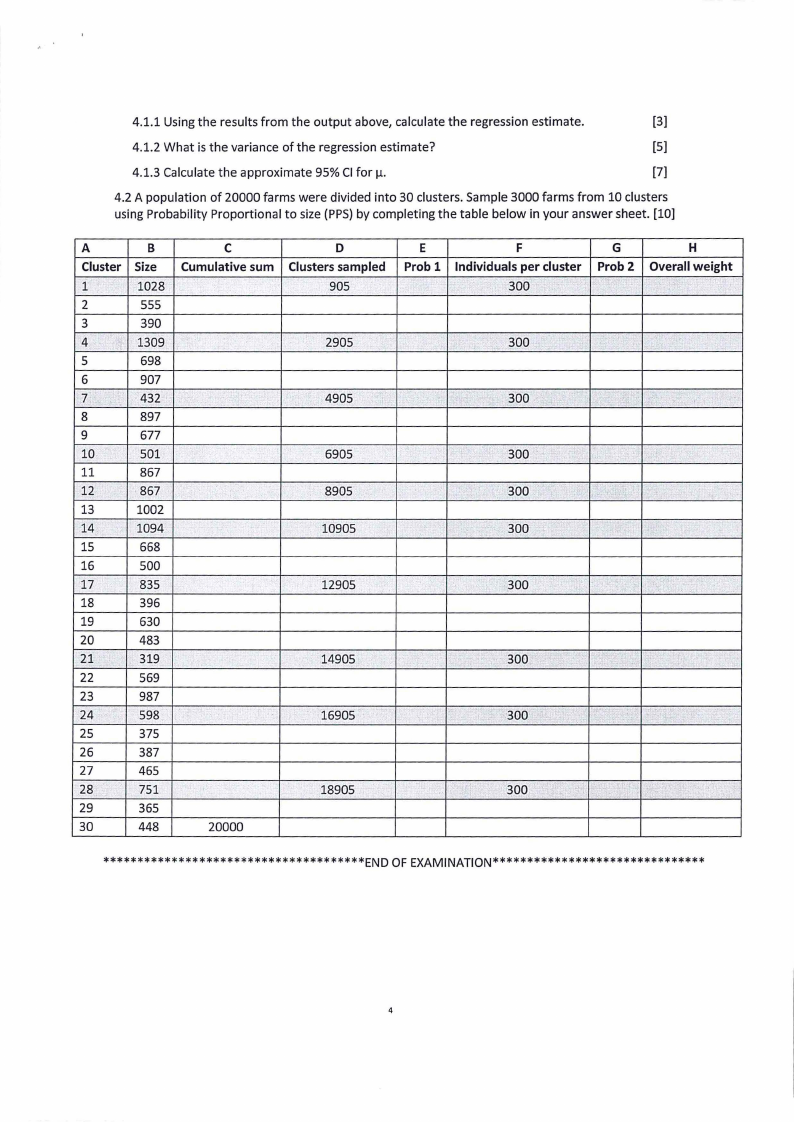
4.1.1 Using the results from the output above, calculate the regression estimate.
[3]
4.1.2 What is the variance of the regression estimate?
[5]
4.1.3 Calculate the approximate 95% Cl forµ.
[7]
4.2 A population of 20000 farms were divided into 30 clusters. Sample 3000 farms from 10 clusters
using Probability Proportional to size (PPS)by completing the table below in your answer sheet. [10]
A
B
Cluster Size
1
1028
2
555
3
390
4
1309
5
698
6
907
7
432
8
897
9
677
10
501
11
867
12
867
13
1002
14
1094
15
668
16
500
17
835
18
396
19
630
20
483
21
319
22
569
23
987
24
598
25
375
26
387
27
465
28
751
29
365
30
448
C
Cumulative sum
D
Clusterssampled
905
2905
4905
6905
8905
10905
12905
14905
.
16905
20000
18905
E
Prob 1
F
Individualsper cluster
300
G
Prob2
300
300
r
.,
300
300
300
-
'
300
· 300
"
·- 300
·,.r.-·· 300
•·
H
Overall weight
•
"'
.. '
..
-
,.
**************************************END OF EXAMINATION*******************************





