 |
SFE612S - STATISTICS FOR ECONOMICS 2B - 2ND OPP - JANUARY 2025 |
 |
1 Page 1 |
▲back to top |

p
nAmlBIA UnlVERSITY
OF SCIEnCEAno TECHnOLOGY
FacultoyfHealthN, atural
ResourcaensdApplied
Sciences
Schoool f NaturalandApplied
Sciences
Departmentof Mathematics,
StatisticsandActuarialScience
13JacksonKaujeuaStreet
PrivateBag13388
Windhoek
NAMIBIA
T: +264612072913
E: msas@nust.na
W: www.nust.na
QUALIFICATIONS: BACHELOR OF ECONOMICS
QUALIFICATION CODE: 07BECO
LEVEL:6
COURSE: STATISTICS FOR ECONOMISTS 2B
COURSECODE: SFE612S
DATE: JANUARY 2025
SESSION: 1
DURATION: 3 HOURS
MARKS: 100
SECONDOPPORTUNITY/SUPPLEMENTARYE: XAMINATION QUESTIONPAPER
EXAMINER:
MODERATOR:
MR GABRIEL S MBOKOMA
MR ETUHOLE MWAHI
INSTRUCTIONS:
1. Answer all questions on the separate answer sheet.
2. Please write neatly and legibly.
3. Do not use the left side margin of the exam paper. This must be allowed for the
examiner.
4. No books, notes and other additional aids are allowed.
5. Mark all answers clearly with their respective question numbers.
PERMISSIBLEMATERIALS:
1. Non-Programmable Calculator
2. Attached statistical tables (t-table, x 2 -table and F-table).
This paper consists of 4 pages including this front page.
 |
2 Page 2 |
▲back to top |

QUESTION 1 [20 MARKS)
Marlon Motors has three cars of the same make and model in stock. They would like to
compare the fuel consumption ofthe three cars (labeled A, B, and C) using four different types
of petrol. For each trial, 4 litres of petrol was added to empty tank, and car was driven until it
completely ran out of petrol. The following table shows the number of kilometers driven in
each trial.
Types of petrol
Regular
Super Regular
Unleaded
Premium Unleaded
Fuel consumption by three cars
CARA
CAR B
CARC
22.4
20.8
21.5
17
19.4
20.7
19.2
20.2
21.2
20.3
18.6
20.4
1.1 Construct an appropriate two-way ANOVA table for these data.
[12]
1.2 Determine whether the fuel consumption of the three cars is affected by four
different types of petrol at 5% level.
[8]
QUESTION 2 [15 MARKS)
The number of goals scored by a football team is recorded for 100 games. The results are
summarised in table below:
Number of goals
0
1
2
3
4
Frequency
40
33
14
8
5
2.1 Calculate the mean number of goals scored per game.
[2]
2.2 The manager claimed that the number of goals scored per match follows a Poisson
distribution. He used the answer in part (2.1) to calculate the expected frequencies
given in the table below.
Number of goals Expected frequency (fe)
0
34.994
1
X
2
y
3
6.752
~4
2.221
Statistics for Economists 2B (SFE612S)
2nd Opportunity January 2025
2
 |
3 Page 3 |
▲back to top |

2.2.1 Find the value of x and y, give your answers to 3 decimal places.
[4]
2.2.2 Use a 5% level of significance to test the manager's claim
[8]
QUESTION 3 [25 MARKS]
A police authority conducts an eight-week experiment. In each week, it records the number
of foot patrols x made in small town and the number of reported crimes y in that town. The
data are summarised as follows:
L x = 52, :2x: 2 = 380, :2y: = 225, :2y: 2 = 7007, :2x:y = 1335, n = 8
3.1 Compute the Pearson correlation coefficient and interpret it.
[4]
3.2 Use appropriate hypothesis t-test to determine whether the correlation coefficient is
significant at 5% level
[5]
3.3 Fit a simple linear regression model for predicting y given x.
[5]
3.4 Compute the coefficient of determination and interpret it
[3]
3.5 Compute the standard error of the estimate.
[2]
= 3.6 Construct the 95% prediction interval for y given x 3.
[6]
QUESTION 4 [10 MARKS]
The following information was recorded about the sales of food items from Pick-n-Pay:
Number of items sold (dozen)
Price per item($)
Item
2013
2014
2013
2014
2kg Flour
6.0
7.5
12.20
15.00
1kg Liver
7.5
7.0
40.50
55.00
1kg Jam
14.0
13.5
14.95
20.50
2kg mealie-real
5.0
4.5
13.40
15.50
2L cooking oil
3.0
3.0
26.00
34.00
1.1 Use Laspeyres' approach to calculate composite quantity index for the item sold for
2014 with 2013 as the base year and interpret it.
[5]
1.2 Use Paasche's approach to calculate composite price index for these items for 2014
with 2013 as the base year and interpret it.
[5]
Statistics for Economists 2B (SFE612S}
2nd Opportunity January 2025
3
 |
4 Page 4 |
▲back to top |

QUESTION 5 (30 MARKS)
The table below shows the quarterly sales (in NAD '000') for HB holdings limited from 2015
to 2017.
Quarter
1
2
3
4
2015
35
45
65
33
Year
2016
45
59
89
79
2017
37
53
32
67
5.1 Compute the 4-period centered moving average and the seasonal ratios.
[12]
5.2 Compute the adjusted seasonal indexes for these quarterly sales.
[10]
5.3 Compute the de-seasonalised quarterly sales.
[6]
5.4 Interpret the de-seasonalised 3rd quarter sales for 2016.
[2]
__________
END OF QUESTION PAPER_________
_
Statistics for Economists 28 (SFE612S)
2nd Opportunity January 2025
4
 |
5 Page 5 |
▲back to top |
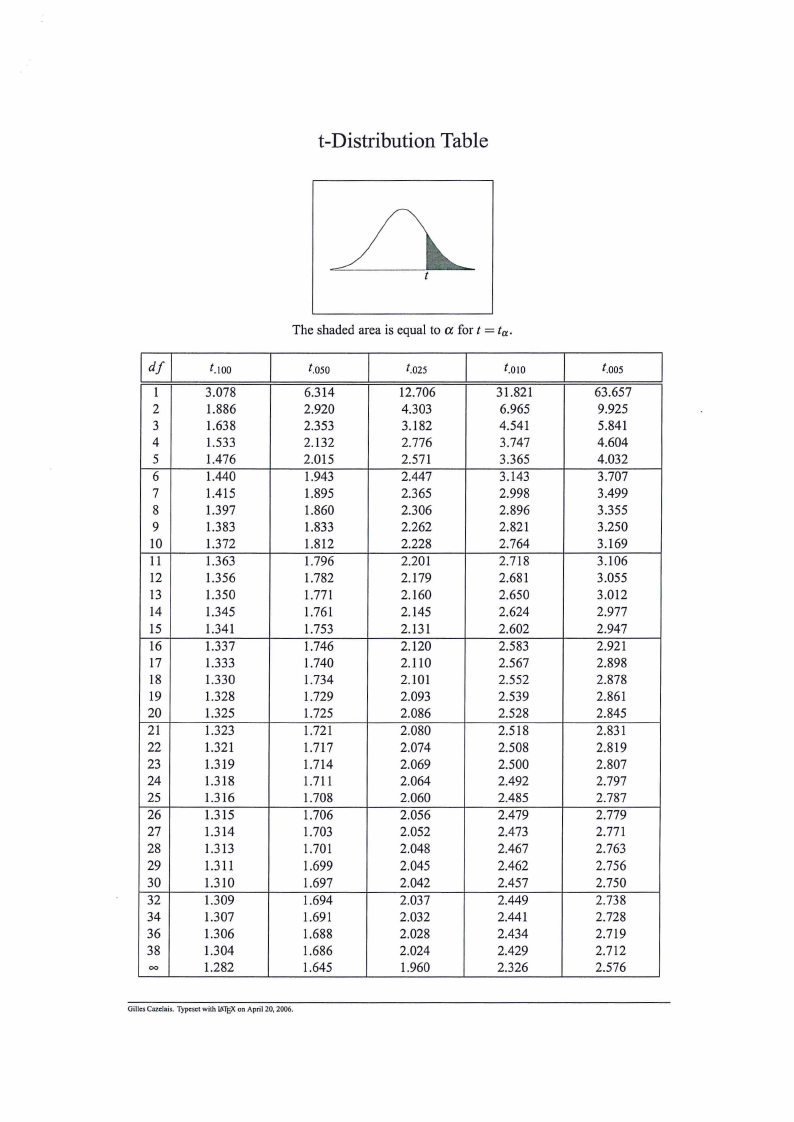
t-DistributionTable
The shaded area is equal to a fort= ta,
t.100
l
3.078
2
l.886
3
l.638
4
1.533
5
l.476
6
l.440
7
l.415
8
l.397
9
l.383
10
l.372
11
1.363
12
l.356
13
1.350
14
l.345
15
l.341
16
l.337
17
1.333
18
l.330
19
1.328
20
1.325
21
l.323
22
l.321
23
l.319
24
1.318
25
1.316
26
1.315
27
l.314
28
l.313
29
l.311
30
l.310
32
l.309
34
l.307
36
l.306
38
1.304
00
1.282
l.050
6.314
2.920
2.353
2.132
2.015
l.943
l.895
l.860
1.833
l.812
l.796
l.782
l.771
l.761
l.753
l.746
l.740
1.734
l.729
l.725
l.721
l.717
l.714
l.711
l.708
l.706
1.703
l.701
l.699
l.697
l.694
l.691
1.688
1.686
l.645
t.025
12.706
4.303
3.182
2.776
2.571
2.447
2.365
2.306
2.262
2.228
2.201
2.179
2.160
2.145
2.131
2.120
2.110
2.101
2.093
2.086
2.080
2.074
2.069
2.064
2.060
2.056
2.052
2.048
2.045
2.042
2.037
2.032
2.028
2.024
l.960
t.010
31.821
6.965
4.541
3.747
3.365
3.143
2.998
2.896
2.821
2.764
2.718
2.681
2.650
2.624
2.602
2.583
2.567
2.552
2.539
2.528
2.518
2.508
2.500
2.492
2.485
2.479
2.473
2.467
2.462
2.457
2.449
2.441
2.434
2.429
2.326
GillesCazclais. Typesetwith k\\TE)Con April20, 2006.
t.005
63.657
9.925
5.841
4.604
4.032
3.707
3.499
3.355
3.250
3.169
3.106
3.055
3.012
2.977
2.947
2.921
2.898
2.878
2.861
2.845
2.831
2.819
2.807
2.797
2.787
2.779
2.771
2.763
2.756
2.750
2.738
2.728
2.719
2.712
2.576
 |
6 Page 6 |
▲back to top |
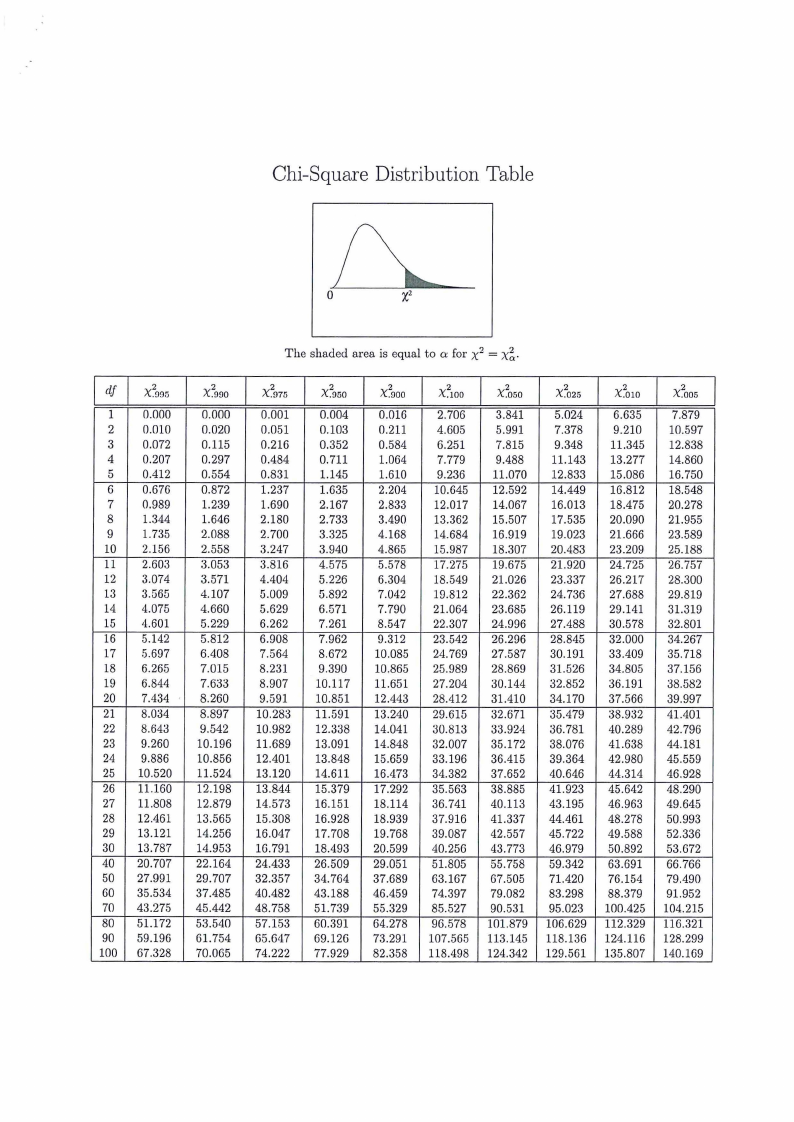
Chi-Square Distribution Table
o
x2
The shaded area is equal to a: for x2 = x~-
df
X~<JD5 X~nno
X297.5
1 0.000
2 0.010
3 0.072
4 0.207
5 0.412
6 0.676
7 0.989
8 1.344
9 1.735
10 2.156
11 2.603
12 3.074
13 3.565
14 4.075
15 4.601
16 5.142
17 5.697
18 6.265
19 6.844
20 7.434
21 8.034
22 8.643
23 9.260
24 9.886
25 10.520
26 11.160
27 11.808
28 12.461
29 13.121
30 13.787
40 20.707
50 27.991
60 35.534
70 43.275
80 51.172
90 59.196
100 67.328
0.000
0.020
0.115
0.297
0.554
0.872
1.239
1.646
2.088
2.558
3.053
3.571
4.107
4.660
5.229
5.812
6.408
7.015
7.633
8.260
8.897
9.542
10.196
10.856
11.524
12.198
12.879
13.565
14.256
14.953
22.164
29.707
37.485
45.442
53.540
61.754
70.065
0.001
0.051
0.216
0.484
0.831
1.237
1.690
2.180
2.700
3.247
3.816
4.404
5.009
5.629
6.262
6.908
7.564
8.231
8.907
9.591
10.283
10.982
11.689
12.401
13.120
13.844
14.573
15.308
16.047
16.791
24.433
32.357
40.482
48.758
57.153
65.647
74.222
X~nso
0.004
0.103
0.352
0.711
1.145
1.635
2.167
2.733
3.325
3.940
4.575
5.226
5.892
6.571
7.261
7.962
8.672
9.390
10.117
10.851
11.591
12.338
13.091
13.848
14.611
15.379
16.151
16.928
17.708
18.493
26.509
34.764
43.188
51.739
60.391
69.126
77.929
X~noo
0.016
0.211
0.584
1.064
1.610
2.204
2.833
3.490
4.168
4.865
5.578
6.304
7.042
7.790
8.547
9.312
10.085
10.865
11.651
12.443
13.240
14.041
14.848
15.659
16.473
17.292
18.114
18.939
19.768
20.599
29.051
37.689
46.459
55.329
64.278
73.291
82.358
X~100
2.706
4.605
6.251
7.779
9.236
10.645
12.017
13.362
14.684
15.987
17.275
18.549
19.812
21.064
22.307
23.542
24.769
25.989
27.204
28.412
29.615
30.813
32.007
33.196
34.382
35.563
36.741
37.916
39.087
40.256
51.805
63.167
74.397
85.527
96.578
107.565
118.498
X~oso
3.841
5.991
7.815
9.488
11.070
12.592
14.067
15.507
16.919
18.307
19.675
21.026
22.362
23.685
24.996
26.296
27.587
28.869
30.144
31.410
32.671
33.924
35.172
36.415
37.652
38.885
40.113
41.337
42.557
43.773
55.758
67.505
79.082
90.531
101.879
113.145
124.342
X202s
5.024
7.378
9.348
11.143
12.833
14.449
16.013
17.535
19.023
20.483
21.920
23.337
24.736
26.119
27.488
28.845
30.191
31.526
32.852
34.170
35.479
36.781
38.076
39.364
40.646
41.923
43.195
44.461
45.722
46.979
59.342
71.420
83.298
95.023
106.629
118.136
129.561
X~o10
6.635
9.210
11.345
13.277
15.086
16.812
18.475
20.090
21.666
23.209
24.725
26.217
27.688
29.141
30.578
32.000
33.409
34.805
36.191
37.566
38.932
40.289
41.638
42.980
44.314
45.642
46.963
48.278
49.588
50.892
63.691
76.154
88.379
100.425
112.329
124.116
135.807
X~oos
7.879
10.597
12.838
14.860
16.750
18.548
20.278
21.955
23.589
25.188
26.757
28.300
29.819
31.319
32.801
34.267
35.718
37.156
38.582
39.997
41.401
42.796
44.181
45.559
46.928
48.290
49.645
50.993
52.336
53.672
66.766
79.490
91.952
104.215
116.321
128.299
140.169
 |
7 Page 7 |
▲back to top |
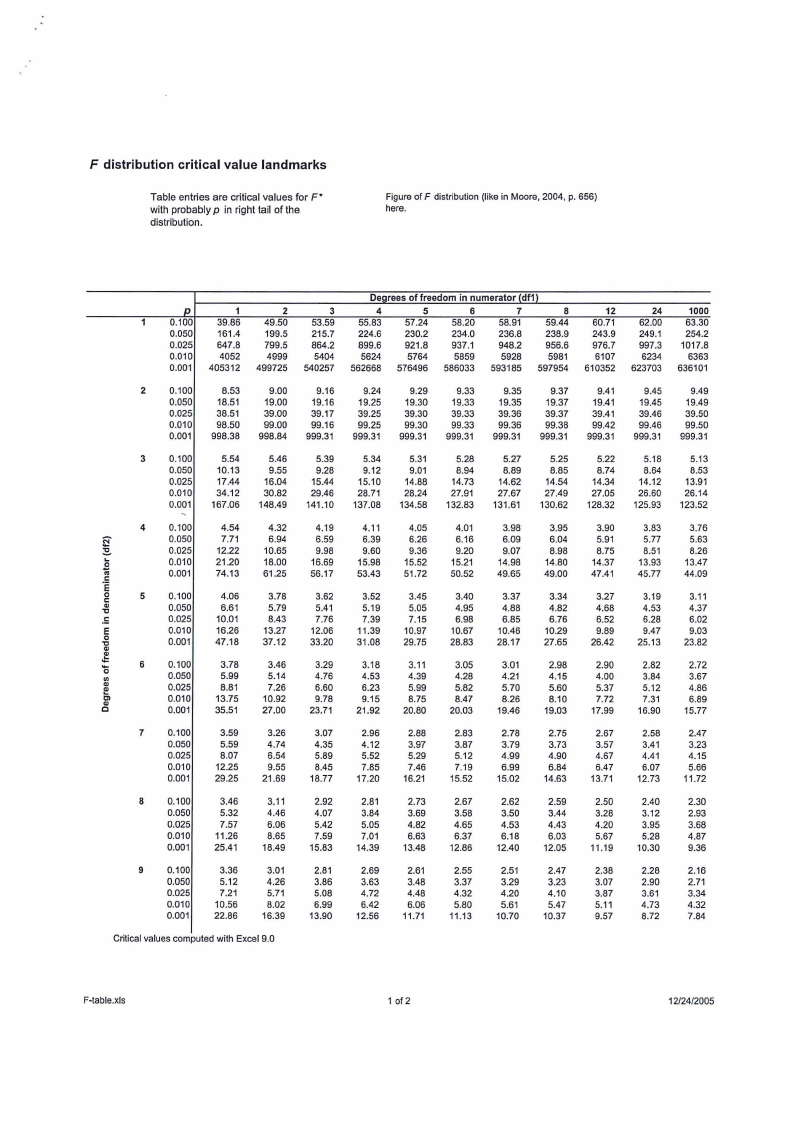
F distribution critical value landmarks
Table entries are critical values for F*
with probably p in right tail of the
distribution.
Figure of F distribution (like in Moore, 2004, p. 656)
here.
0.100
0.050
0.025
0.010
0.001
1
39.86
161.4
647.8
4052
405312
2
49.50
199.5
799.5
4999
499725
3
53.59
215.7
864.2
5404
540257
De rees of freedom in numerator df1
4
5
6
7
8
55.83
57.24
58.20
58.91
59.44
224.6
230.2
234.0
236.8
238.9
899.6
921.8
937.1
948.2
956.6
5624
5764
5859
5928
5981
562668 576496 586033 593185 597954
12
60.71
243.9
976.7
6107
610352
24
62.00
249.1
997.3
6234
623703
1000
63.30
254.2
1017.8
6363
636101
2 0.100
8.53
9.00
9.16
9.24
9.29
9.33
9.35
9.37
9.41
9.45
9.49
0.050
18.51
19.00
19.16
19.25
19.30
19.33
19.35
19.37
19.41
19.45
19.49
0.025
38.51
39.00
39.17
39.25
39.30
39.33
39.36
39.37
39.41
39.46
39.50
0.010
98.50
99.00
99.16
99.25
99.30
99.33
99.36
99.38
99.42
99.46
99.50
0.001 998.38 998.84 999.31 999.31 999.31 999.31 999.31 999.31 999.31 999.31 999.31
3 0.100
5.54
5.46
5.39
5.34
5.31
5.28
5.27
5.25
5.22
5.18
5.13
0.050
10.13
9.55
9.28
9.12
9.01
8.94
8.89
8.85
8.74
8.64
8.53
0.025
17.44
16.04
15.44
15.10
14.88
14.73
14.62
14.54
14.34
14.12
13.91
0.010
34.12
30.82
29.46
28.71
28.24
27.91
27.67
27.49
27.05
26.60
26.14
0.001 167.06 148.49 141.10 137.08 134.58 132.83 131.61 130.62 128.32 125.93 123.52
4
...
0
iu
·eC:
0
C:
5
Q)
,:,
.!:
E
,:0,
Q)
... 6
0
"'Q)
Cl
Q)
C
0.100
0.050
0.025
0.010
0.001
0.100
0.050
0.025
0.010
0.001
0.100
0.050
0.025
0.010
0.001
4.54
7.71
12.22
21.20
74.13
4.06
6.61
10.01
16.26
47.18
3.78
5.99
8.81
13.75
35.51
4.32
6.94
10.65
18.00
61.25
3.78
5.79
8.43
13.27
37.12
3.46
5.14
7.26
10.92
27.00
4.19
6.59
9.98
16.69
56.17
3.62
5.41
7.76
12.06
33.20
3.29
4.76
6.60
9.78
23.71
4.11
6.39
9.60
15.98
53.43
3.52
5.19
7.39
11.39
31.08
3.18
4.53
6.23
9.15
21.92
4.05
6.26
9.36
15.52
51.72
3.45
5.05
7.15
10.97
29.75
3.11
4.39
5.99
8.75
20.80
4.01
6.16
9.20
15.21
50.52
3.40
4.95
6.98
10.67
28.83
3.05
4.28
5.82
8.47
20.03
3.98
6.09
9.07
14.98
49.65
3.37
4.88
6.85
10.46
28.17
3.01
4.21
5.70
8.26
19.46
3.95
6.04
8.98
14.80
49.00
3.34
4.82
6.76
10.29
27.65
2.98
4.15
5.60
8.10
19.03
3.90
5.91
8.75
14.37
47.41
3.27
4.68
6.52
9.89
26.42
2.90
4.00
5.37
7.72
17.99
3.83
5.77
8.51
13.93
45.77
3.19
4.53
6.28
9.47
25.13
2.82
3.84
5.12
7.31
16.90
3.76
5.63
8.26
13.47
44.09
3.11
4.37
6.02
9.03
23.82
2.72
3.67
4.86
6.89
15.77
7 0.100
3.59
3.26
3.07
2.96
2.88
2.83
2.78
2.75
2.67
2.58
2.47
0.050
5.59
4.74
4.35
4.12
3.97
3.87
3.79
3.73
3.57
3.41
3.23
0.025
8.07
6.54
5.89
5.52
5.29
5.12
4.99
4.90
4.67
4.41
4.15
0.010
12.25
9.55
8.45
7.85
7.46
7.19
6.99
6.84
6.47
6.07
5.66
0.001
29.25
21.69
18.77
17.20
16.21
15.52
15.02
14.63
13.71
12.73
11.72
8 0.100
3.46
3.11
2.92
2.81
2.73
2.67
2.62
2.59
2.50
2.40
2.30
0.050
5.32
4.46
4.07
3.84
3.69
3.58
3.50
3.44
3.28
3.12
2.93
0.025
7.57
6.06
5.42
5.05
4.82
4.65
4.53
4.43
4.20
3.95
3.68
0.010
11.26
8.65
7.59
7.01
6.63
6.37
6.18
6.03
5.67
5.28
4.87
0.001
25.41
18.49
15.83
14.39
13.48
12.86
12.40
12.05
11.19
10.30
9.36
9 0.100
3.36
3.01
2.81
2.69
2.61
2.55
2.51
2.47
2.38
2.28
2.16
0.050
5.12
4.26
3.86
3.63
3.48
3.37
3.29
3.23
3.07
2.90
2.71
0.025
7.21
5.71
5.08
4.72
4.48
4.32
4.20
4.10
3.87
3.61
3.34
0.010
10.56
8.02
6.99
6.42
6.06
5.80
5.61
5.47
5.11
4.73
4.32
0.001
22.86
16.39
13.90
12.56
11.71
11.13
10.70
10.37
9.57
8.72
7.84
Critical values computed with Excel 9.0
F-table.xls
1 of 2
12/24/2005
 |
8 Page 8 |
▲back to top |
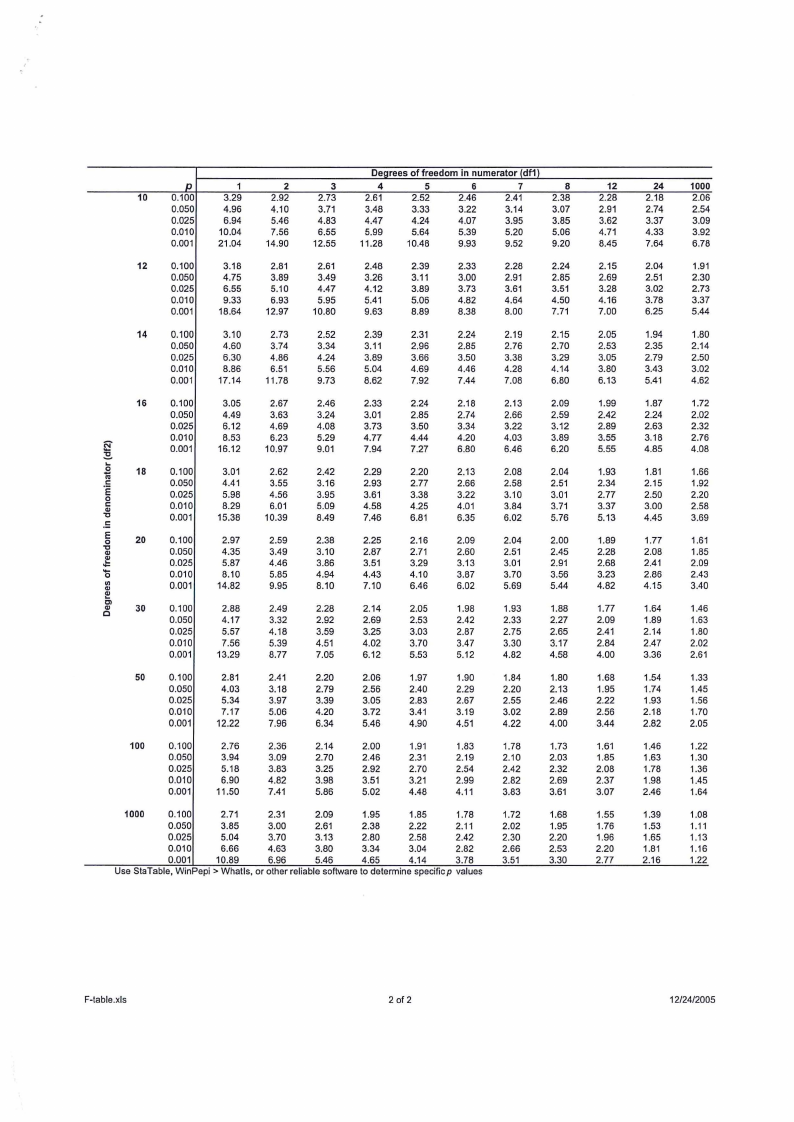
Dei:irees of freedom in numerator (df1 l
D
1
2
3
4
5
6
7
8
10 0.100
3.29
2.92
2.73
2.61
2.52
2.46
2.41
2.38
0.050
4.96
4.10
3.71
3.48
3.33
3.22
3.14
3.07
0.025
6.94
5.46
4.83
4.47
4.24
4.07
3.95
3.85
0.010
10.04
7.56
6.55
5.99
5.64
5.39
5.20
5.06
0.001
21.04
14.90
12.55
11.28
10.48
9.93
9.52
9.20
12
0.100
3.18
2.81
2.61
2.48
2.39
2.33
2.28
2.24
0.050
4.75
3.89
3.49
3.26
3.11
3.00
2.91
2.85
0.025
6.55
5.10
4.47
4.12
3.89
3.73
3.61
3.51
0.010
9.33
6.93
5.95
5.41
5.06
4.82
4.64
4.50
0.001
18.64
12.97
10.80
9.63
8.89
8.38
8.00
7.71
14
0.100
3.10
2.73
2.52
2.39
2.31
2.24
2.19
2.15
0.050
4.60
3.74
3.34
3.11
2.96
2.85
2.76
2.70
0.025
6.30
4.86
4.24
3.89
3.66
3.50
3.38
3.29
0.010
8.86
6.51
5.56
5.04
4.69
4.46
4.28
4.14
0.001
17.14
11.78
9.73
8.62
7.92
7.44
7.08
6.80
16 0.100
3.05
2.67
2.46
2.33
2.24
2.18
2.13
2.09
0.050
4.49
3.63
3.24
3.01
2.85
2.74
2.66
2.59
0.025
6.12
4.69
4.08
3.73
3.50
3.34
3.22
3.12
er
0.010
8.53
6.23
5.29
4.77
4.44
4.20
4.03
3.89
0.001
16.12
10.97
9.01
7.94
7.27
6.80
6.46
6.20
...
18 0.100
3.01
2.62
2.42
2.29
2.20
2.13
2.08
2.04
.C E
0.050
4.41
3.55
3.16
2.93
2.77
2.66
2.58
2.51
0C.,
0.025
5.98
4.56
3.95
3.61
3.38
3.22
3.10
3.01
0.010
8.29
6.01
5.09
4.58
4.25
4.01
3.84
3.71
'tJ
0.001
15.38
10.39
8.49
7.46
6.81
6.35
6.02
5.76
.5
E
't0..J,,
20
0.100
0.050
2.97
4.35
2.59
3.49
2.38
3.10
2.25
2.87
2.16
2.71
2.09
2.60
2.04
2.51
2.00
2.45
0.025
5.87
4.46
3.86
3.51
3.29
3.13
3.01
2.91
0
0.010
8.10
5.85
4.94
4.43
4.10
3.87
3.70
3.56
.,(/)
0.001
14.82
9.95
8.10
7.10
6.46
6.02
5.69
5.44
:".!,!'
C
30
0.100
0.050
2.88
4.17
2.49
3.32
2.28
2.92
2.14
2.69
2.05
2.53
1.98
2.42
1.93
2.33
1.88
2.27
0.025
5.57
4.18
3.59
3.25
3.03
2.87
2.75
2.65
0.010
7.56
5.39
4.51
4.02
3.70
3.47
3.30
3.17
0.001
13.29
8.77
7.05
6.12
5.53
5.12
4.82
4.58
50
0.100
2.81
2.41
2.20
2.06
1.97
1.90
1.84
1.80
0.050
4.03
3.18
2.79
2.56
2.40
2.29
2.20
2.13
0.025
5.34
3.97
3.39
3.05
2.83
2.67
2.55
2.46
0.010
7.17
5.06
4.20
3.72
3.41
3.19
3.02
2.89
0.001
12.22
7.96
6.34
5.46
4.90
4.51
4.22
4.00
100
0.100
2.76
2.36
2.14
2.00
1.91
1.83
1.78
1.73
0.050
3.94
3.09
2.70
2.46
2.31
2.19
2.10
2.03
0.025
5.18
3.83
3.25
2.92
2.70
2.54
2.42
2.32
0.010
6.90
4.82
3.98
3.51
3.21
2.99
2.82
2.69
0.001
11.50
7.41
5.86
5.02
4.48
4.11
3.83
3.61
1000
0.100
2.71
2.31
2.09
1.95
1.85
1.78
1.72
1.68
0.050
3.85
3.00
2.61
2.38
2.22
2.11
2.02
1.95
0.025
5.04
3.70
3.13
2.80
2.58
2.42
2.30
2.20
0.010
6.66
4.63
3.80
3.34
3.04
2.82
2.66
2.53
0.001
10.89
6.96
5.46
4.65
4.14
3.78
3.51
3.30
Use StaTable, W1nPep1> Whatls, or other reliable software to determine spec1ficp values
12
2.28
2.91
3.62
4.71
8.45
2.15
2.69
3.28
4.16
7.00
2.05
2.53
3.05
3.80
6.13
1.99
2.42
2.89
3.55
5.55
1.93
2.34
2.77
3.37
5.13
1.89
2.28
2.68
3.23
4.82
1.77
2.09
2.41
2.84
4.00
1.68
1.95
2.22
2.56
3.44
1.61
1.85
2.08
2.37
3.07
1.55
1.76
1.96
2.20
2.77
24
2.18
2.74
3.37
4.33
7.64
2.04
2.51
3.02
3.78
6.25
1.94
2.35
2.79
3.43
5.41
1.87
2.24
2.63
3.18
4.85
1.81
2.15
2.50
3.00
4.45
1.77
2.08
2.41
2.86
4.15
1.64
1.89
2.14
2.47
3.36
1.54
1.74
1.93
2.18
2.82
1.46
1.63
1.78
1.98
2.46
1.39
1.53
1.65
1.81
2.16
1000
2.06
2.54
3.09
3.92
6.78
1.91
2.30
2.73
3.37
5.44
1.80
2.14
2.50
3.02
4.62
1.72
2.02
2.32
2.76
4.08
1.66
1.92
2.20
2.58
3.69
1.61
1.85
2.09
2.43
3.40
1.46
1.63
1.80
2.02
2.61
1.33
1.45
1.56
1.70
2.05
1.22
1.30
1.36
1.45
1.64
1.08
1.11
1.13
1.16
1.22
F-table.xls
2 of 2
12/24/2005





