 |
MMO702S - MATHEMATICAL MODELLING 2- 1ST OPP - NOVEMBER - 2024 |
 |
1 Page 1 |
▲back to top |

n Am I BI A u ni VE Rs ITY
OF SCIEnCE
Facultyof Health,Natural
ResourceasndApplied
Sciences
Schoolof Natural andApplied
Sciences
Department of Mathematics,
Statistics and Actuarial Science
13JacksonKaujeuaStreet
Private Bag 13388
Windhoek
NAMIBIA
T: +264612072913
E: msas@nust.na
IN: wv1w.nust.na
QUALIFICATION: BACHELOR of SCIENCE IN APPLIED MATHEMATICS AND STATISTICS
QUALIFICATION CODE: 07BSAM
LEVEL: 7
COURSE:MATHEMATICAL MODELLING 2
COURSECODE: MMO702S
DATE: NOVEMBER 2024
SESSION: 1
DURATION: 3 HOURS
MARKS: 150 (To be converted to 100%)
EXAMINER:
MODERATOR:
FIRST OPPORTUNITY: EXAMINATION QUESTION PAPER
Prof Sunday A. Reju
Prof O/uwole D. Makinde
INSTRUCTIONS
1. Answer all questions on the separate answer sheet.
2. Please write neatly and legibly.
3. Do not use the left side margin of the exam paper. This must be allowed for the
examiner.
4. No books, notes and other additional aids are allowed.
5. Mark all answers clearly with their respective question numbers.
6. Use of COMMA is NOT ALLOWED for a DECIMAL POINT.
PERMISSIBLE MATERIALS
1. Non-Programmable Calculator
ATTACHMENTS
NONE
This paper consists of 3 pages including this front page.
 |
2 Page 2 |
▲back to top |
QUESTION 1 [30 MARKS]
(a) Comprehensively discuss Post-optimality analysis in linear optimisation modelling and
the basic question it answers.
(3 Marks)
(b) A college hostel furniture maker realises a net unit profit of $25 per desk and $30 per
locker. Assume that he has up to 680 metres of wood to devote weekly to the project
and up to 125 hours of labour. He estimates that it requires 20 metres of wood and 5
hours of labour to complete a desk and 30 metres of wood and 3 hours of labour for a
locker. Moreover, he has signed contracts to deliver two desks and one locker every
week. Formulate and solve the model maximizing his profits for desks and lockers.
(7 Marks)
(c) Define post-optimality analysis for the problem defined in (b) and hence discuss the
analyses for changes in his profits on both lockers and desks stating your observations for
the two furniture items and providing a summary for your two analyses.
(10.5 Marks)
(d) State the mathematical definition of RELIABILITY and its expression. Specifically
describe Serial and Parallel systems and their reliability equations. Hence for a system
whose component reliabilities are 0.94 and 0.97, determine the system reliability when
the components are assembled serially and in parallel, stating your observations for the
two assemblies.
(9.5 Marks)
QUESTION 2 [60 MARKS]
(a) Discuss the basic characteristics of Queuing system and state three basic performance
measures of the system.
(10 Marks)
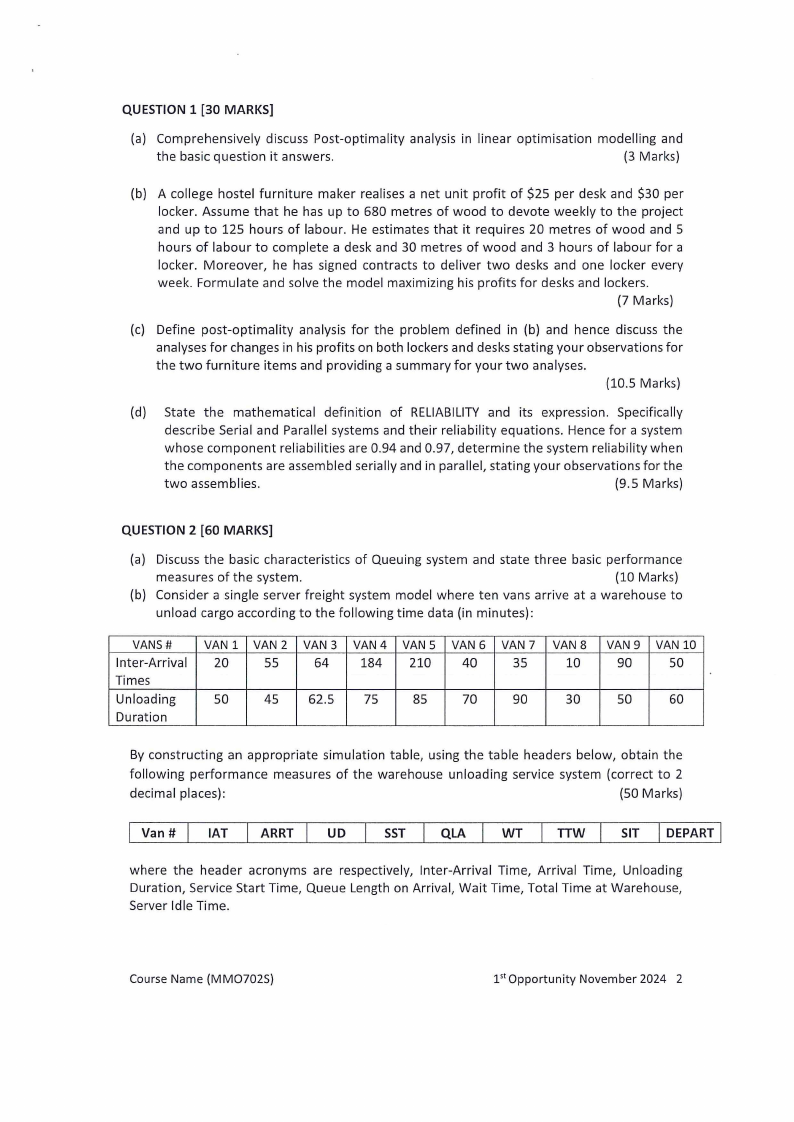
(b) Consider a single server freight system model where ten vans arrive at a warehouse to
unload cargo according to the following time data (in minutes):
VANS#
Inter-Arrival
Times
Unloading
Duration
VAN 1 VAN 2 VAN 3 VAN4 VAN 5 VAN 6 VAN 7 VAN 8 VAN 9 VAN 10
20
55
64
184 210
40
35
10
90
so
so 45 62.5 75
85
70
90
30
so 60
By constructing an appropriate simulation table, using the table headers below, obtain the
following performance measures of the warehouse unloading service system (correct to 2
decimal places):
(SO Marks)
I Van# I IAT I ARRT
UD
SST
QLA
WT
TTW
SIT I DEPART I
where the header acronyms are respectively, Inter-Arrival Time, Arrival Time, Unloading
Duration, Service Start Time, Queue Length on Arrival, Wait Time, Total Time at Warehouse,
Server Idle Time.
Course Name (MMO702S)
1st Opportunity November 2024 2
 |
3 Page 3 |
▲back to top |

(i) Average wait time (WT).
(ii) Average unloading duration (UD).
(iii) Average time spent at the warehouse (TTW).
(iv) Percentage of time the server is idle (SIT)
(v) When do the 3rd , 6th and 9th vans leave the warehouse?
QUESTION 3 [20 MARKS]
(a) Discuss Markov Chain and its associated concepts, providing specifically a general 2-state
Markov process representation.
(7 Marks)
(b) Consider a model for the value of a stock. At the end of a given day, the price is recorded.
If the stock has gone up, the probability that it will go up tomorrow is 0.7. If the stock has
gone down, the probability that it will go up tomorrow is only 0.5. Construct an
appropriate transition matrix for the 2-state Markov process model for the fluctuating
stock problem and using appropriate percentage variables and their definitions, formulate
the model equations to determine the long-term percentage increase and decrease for
the stock problem.
(13 Marks)
QUESTION 4 [40 MARKS]
(a) A spring with a mass of 2kg has natural length 0.5m. A force of 25.6N is required to
maintain it stretched to a length of 0.7m and then released with initial velocity 0, find the
position of the mass at any time t, stating all physical laws to support the fundamental
equations and associated concepts of your model and its solution before using the given data.
(14 Marks)
(b) Suppose a large lake that was formed by damming a river holds initially 100 million
gallons of water. Because a nearby agricultural field was sprayed with a pesticide, the water
has become contaminated. The concentration of the pesticide has been measured and is
equal to 35ppm (parts per million), or 35 x 10·6• The river continues to flow into the lake at a
rate of 300 gal/min. The river is only slightly contaminated with a pesticide and has a
concentration of 5 ppm. The flow of water over the dam can be controlled and is set at 400
gal/min. Assume that no additional spraying causes the lake to become even more
contaminated. How long will it be before the water reaches an acceptable level of
concentration equal to 15 ppm?
(26 Marks)
END OF QUESTION PAPER
TOTAL MARKS= 150
Course Name (MMO7025)
1'1Opportunity November 2024 3





