 |
AGS520S - AGRICULTURAL STATISTICS - 1ST OPP - JUNE 2024 |
|
|
1 Pages 1-10 |
▲back to top |
|
|
1.1 Page 1 |
▲back to top |
" nAm I BI A Uni VERSITY
OF SCIEnCE Ano TECHn OLOGY
FACULTYOF HEALTH,NATURALRESOURCESAND APPLIEDSCIENCES
DEPARTMENT OF AGRICULTURALSCIENCESAND AGRIBUSINESS
QUALIFICATION: BACHELOR OF SCIENCE IN AGRICULTURE
QUALIFICATION CODE: 07BAGA
LEVEL: 7
COURSE CODE: AGS520S
COURSE NAME: AGRICULTURALSTATISTICS
SESSION: JUNE 2024
DURATION: 3 HOURS
PAPER:1
MARKS: 100
EXAMINER{S)
FIRST OPPORTUNITY EXAMINATION QUESTION PAPER
DR DAVID UCHEZUBA
MODERATOR: MR ANDREW ROUX
INSTRUCTIONS
1. This paper consists of two sections: Section A has 15 multiple-choice questions and 5 True
or False questions. Section Bis made up of four essay-type questions.
2. Answer ALL questions in blue or black ink.
3. Start each question on a new page in your answer booklet.
4. Questions relating to this paper may be raised in the initial 30 minutes after the start of the
examination. Thereafter, students must use their initiative to deal with any perceived error
or ambiguities & any assumption made should be clearly stated.
THIS MEMO CONSISTS OF 13 PAGES (Including this front page)
|
|
1.2 Page 2 |
▲back to top |
SECTIONA
QUESTION1 (20 Marks)
Consider a random variable X with the following probability distribution.
I ~-10
Use the table to answer questions 1.1 to 1.5.
I :.45
1.1.
Find P(X > 4)
A.
0.5
B
0.7
C
0.6
D
0.4
1.2
Find P(X s 4)
A.
0.2
B
0.4
C
0.3
D
0.1
l.3
X <2
A.
0.0
B
0.5
C
0.6
D
0.7
1.4
Consider the claim that the mean weight of airline passengers (including hand luggage) is at
most 43 kg per person. Identify the null and alternative hypothesis used to verify this claim.
A.
H0 : µ = 43 kg, H0 : µ. = 43 kg
2
|
|
1.3 Page 3 |
▲back to top |
B
* H0 : µ = 43 kg, Ha : µ 43 kg
C
Ha : µ = 43 kg, Ha : µ < 43 kg
D
Ha : µ < 43 kg, Ha : µ. > 43 kg
1.5
Assume the claim that the mean weight of airline passengers (including hand luggage) is greater
than 43 kg per person. Identify the null and alternative hypothesis used to verify this claim.
A.
Ha : µ?. 43 kg, Ha : µ > 43 kg
B
Ha : µ?. 43 kg, Ha : µ < 43 kg
C
Ha : µ 43 kg, Ha : µ > 43 kg
D
Ha : µ 43 kg, Ha : µ ?. 43 kg
1.6
Assume the claim that the mean weight of airline passengers (including hand luggage) is less
than 43 kg per person. Identify the null and alternative hypothesis used to verify this claim.
A.
Ha : µ < 43 kg, Ha : µ < 43 kg
B
Ha : µ < 43 kg, Ha : µ?. 43 kg
c
Ha:µ> 43 kg, Ha:µ> 43 kg
D
Ha : µ?. 43 kg, Ha : µ < 43 kg
1.7
Which of the following distributions is not symmetrical around the mean?
A.
t-distribution
B.
Normal distribution
C.
All of the above
D.
Chi-square distribution
1.8
How many per cent under the normal curve lies between µ±CY
A.
99
B.
68
C.
95
D.
97
3
|
|
1.4 Page 4 |
▲back to top |
1.9
The skewness and kurtosis of a normal probability distribution are.
A.
S =3; K = 0
B.
S = O;K = 3
c.
S = O;K = 0
D.
S = 1; K = 3
1.10
We committed a type I error, this means we.
A.
We did not use the t-table corrected
B.
Rejected a true alternative hypothesis
C.
Rejected a true null hypothesis
D.
Rejected a false hypothesis
Given a sample space S = {1, 2, 3, 4, 5, 6}, Let A= {2, 4, 6}and B = {4, 5, 6}. Use this to answer
questions 1.11 to 1.15.
1.11 Find AnB.
A.
{2,5}
B.
{5, 6}
C.
{2,6}
D.
{4, 6}
1.12 Find An B
A.
6
B.
2
C.
5
D.
4
1.13
Find A
A.
{l, 3, 5}
B.
{2, 3, 5}
4
|
|
1.5 Page 5 |
▲back to top |
c.
{2, 3, 4}
D.
{l, 2, 3}
1.14 Find AUE
A.
{ 3, 5, 6}
B.
{ 2, 5, 6}
C.
{ 4, 5, 6}
D.
{2, 4, 5, 6}
1.15 Find AUA
A.
{2,4,6}
B.
{1,2, 3,4, 5,6}
C.
{1,2,3}
D.
{1,2, 3,5, 6}
TRUE OR FALSEQUESTIONS
Indicate whether the following statements are true or false.
1.16 An event that cannot happen has a probability of -1. True or False
1.17 The t-distribution has a zero mean and a standard deviation of 1. True or False
1.18 The values of a chi-square can be zero or positive but never negative True or False
1.19 The mean is sensitive to extreme values (outliers). True or False.
1.20 The height of a person is an example of a continuous data. True or False
5
|
|
1.6 Page 6 |
▲back to top |
SECTION B
QUESTION 2 (20 Marks)
2.1.
For one month, time records show the following results for the number of workers absent
per day.
13
14
9
17
21
10
15
22
19
13
22
13
19
23
17
21
10
9
20
18
For the distribution above calculate the following
2.1.l.
2.1.2.
2.1.3.
2.1.4.
2.1.5
Arithmetic mean
Variance
Standard deviation
Coefficient of variation
Range
(2 Marks)
(2 Marks)
(2 Marks)
(2 Marks)
(2 Marks)
2.2. Assume that z-scores are normally distributed with a mean of 0 and standard deviation of 1.
2.2.l. Find a if P(z <a)= 0.9599
(2 Marks)
2.2.2. Find b if P(z > b) = 0.9772
(2 Marks)
2.2.3. Find c if P(z > c) = 0.0668
(2 Marks)
2.2.4. Find d if P(-d < z < d) = 0.5878
0
(2 Marks)
2.2.5. Find e if P(-e < z < e) = 0.0956
(2 Marks)
QUESTION 3 (20 Marks)
3.1.
Based on the data from the National Health and Nutrition Examination Survey, assume that the
weights of men are normally distributed with a mean of 172 pounds and a standard deviation of
29 pounds.
3.1.l.
Find the probability that if an individual is randomly selected, his weight will be greater than 175
pounds.
(5 Marks)
3.1.2.
Find the probability that 20 randomly selected men will have a mean weight that is greater than
6
|
|
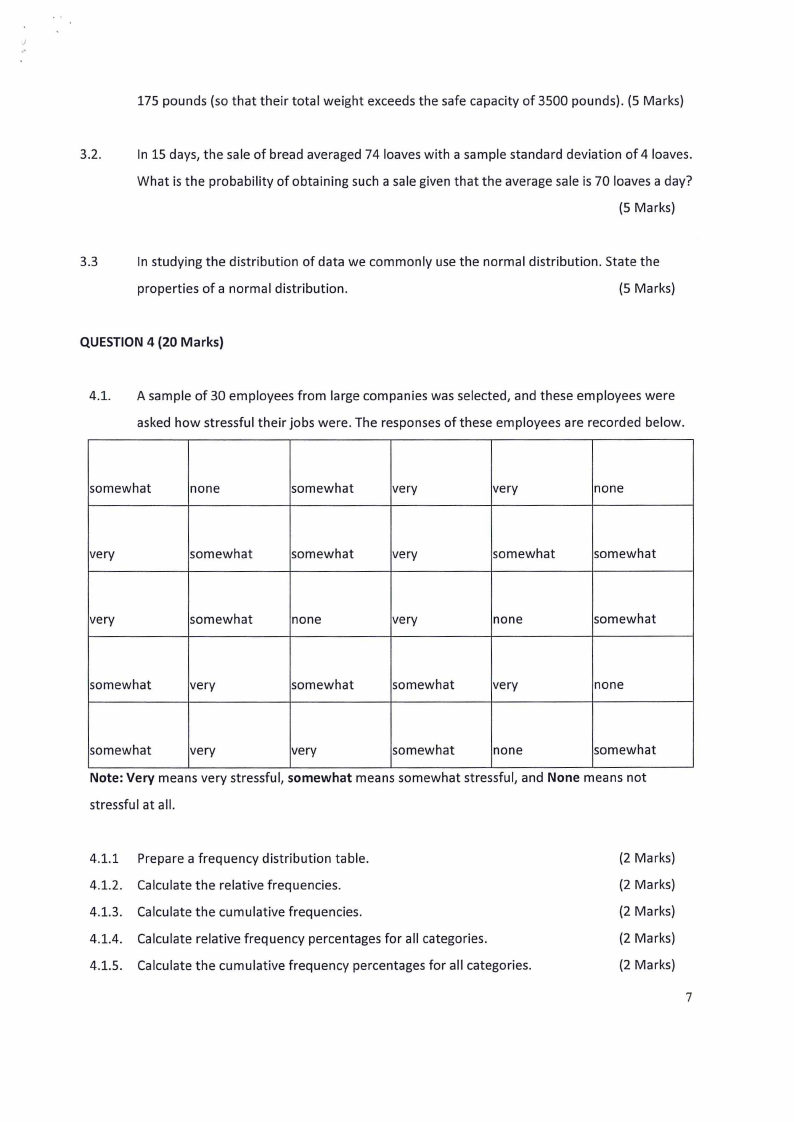
1.7 Page 7 |
▲back to top |
175 pounds (so that their total weight exceeds the safe capacity of 3500 pounds). (5 Marks)
3.2.
In 15 days, the sale of bread averaged 74 loaves with a sample standard deviation of 4 loaves.
What is the probability of obtaining such a sale given that the average sale is 70 loaves a day?
(5 Marks)
3.3
In studying the distribution of data we commonly use the normal distribution. State the
properties of a normal distribution.
(5 Marks)
QUESTION 4 (20 Marks)
4.1. A sample of 30 employees from large companies was selected, and these employees were
asked how stressful their jobs were. The responses of these employees are recorded below.
somewhat
none
somewhat
very
very
none
very
somewhat
somewhat
very
somewhat
somewhat
very
somewhat
none
very
none
somewhat
somewhat
very
somewhat
somewhat
very
none
somewhat
very
very
somewhat
none
somewhat
Note: Very means very stressful, somewhat means somewhat stressful, and None means not
stressful at all.
4.1.1 Prepare a frequency distribution table.
4.1.2. Calculate the relative frequencies.
4.1.3. Calculate the cumulative frequencies.
4.1.4. Calculate relative frequency percentages for all categories.
4.1.5. Calculate the cumulative frequency percentages for all categories.
(2 Marks)
(2 Marks)
(2 Marks)
(2 Marks)
(2 Marks)
7
|
|
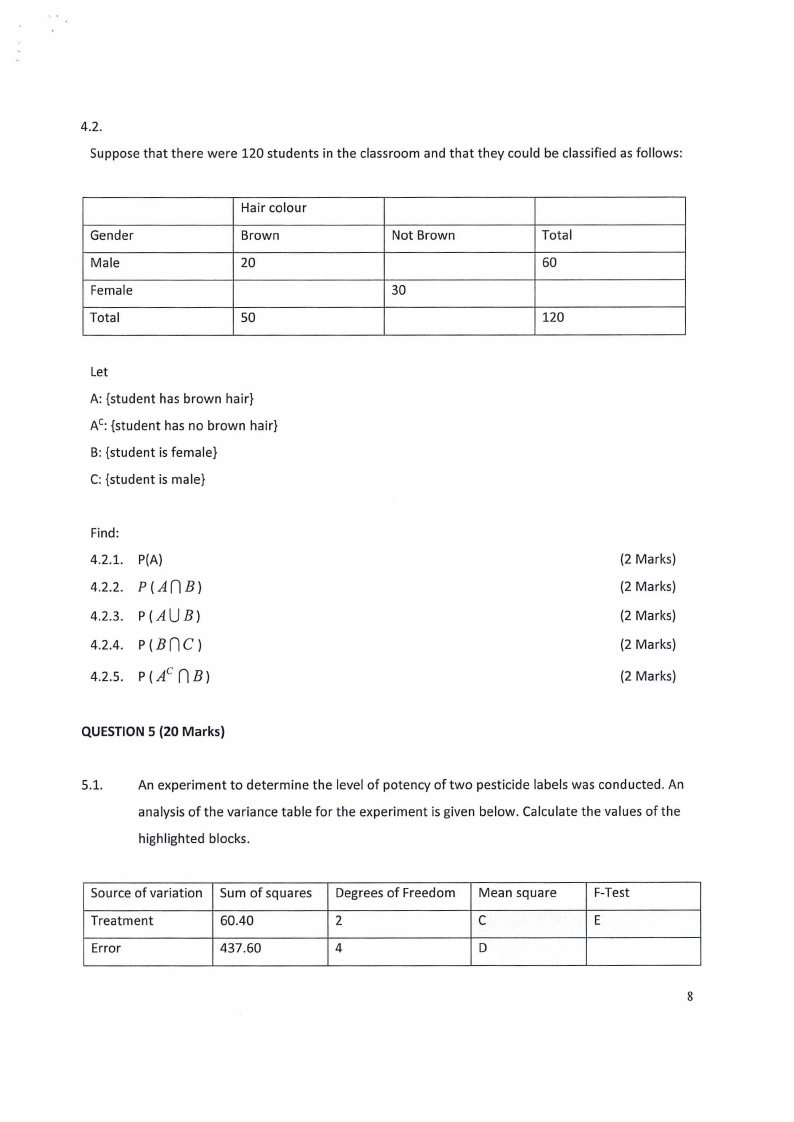
1.8 Page 8 |
▲back to top |
4.2.
Suppose that there were 120 students in the classroom and that they could be classified as follows:
Gender
Male
Female
Total
Hair colour
Brown
20
so
Not Brown
30
Total
60
120
Let
A: {student has brown hair}
Ac: {student has no brown hair}
B: {student is female}
C: {student is male}
Find:
4.2.1. P(A}
4.2.2. P(AnB}
4.2.3. P(AUB}
4.2.4. P(Bnc}
4.2.5. P (Ac n B}
(2 Marks}
(2 Marks)
(2 Marks)
(2 Marks)
(2 Marks)
QUESTION 5 {20 Marks)
5.1.
An experiment to determine the level of potency of two pesticide labels was conducted. An
analysis of the variance table for the experiment is given below. Calculate the values of the
highlighted blocks.
Source of variation
Treatment
Error
Sum of squares
60.40
437.60
Degrees of Freedom
2
4
Mean square
C
D
F-Test
E
8
|
|
1.9 Page 9 |
▲back to top |
I Total
(10 Marks)
5.2.
5.2.1
5.2.2.
The proper operation of a typical home appliance requires electrical voltage levels that do not
vary much. Ten (10) voltage levels are recorded on 10 different days. The 10 values have a mean
= of 123.53 and a standard deviation of s 0.15 volts. Use the sample data to construct a 95 %
confidence interval estimate of the standard deviation of all voltage levels.
(8 Marks)
Interpret your result.
(2 Marks)
STATISTICALFORMULA
2
O'
=--(-x-xY
N-l
/x-X)' CT~
CT~
N-l '
N-l
z=--,x-µ
O'
z = x-µ- X = x-µ- X
a-x
a- ,
z=
x-µ-
X
O' ,
x-µ
t=------'--
2
O'
=--(-x-x)
N-l '
t = _(x_-_µ=-)
x-x
O'=--
n-l'
z=-- x-µ
a-
9
|
|
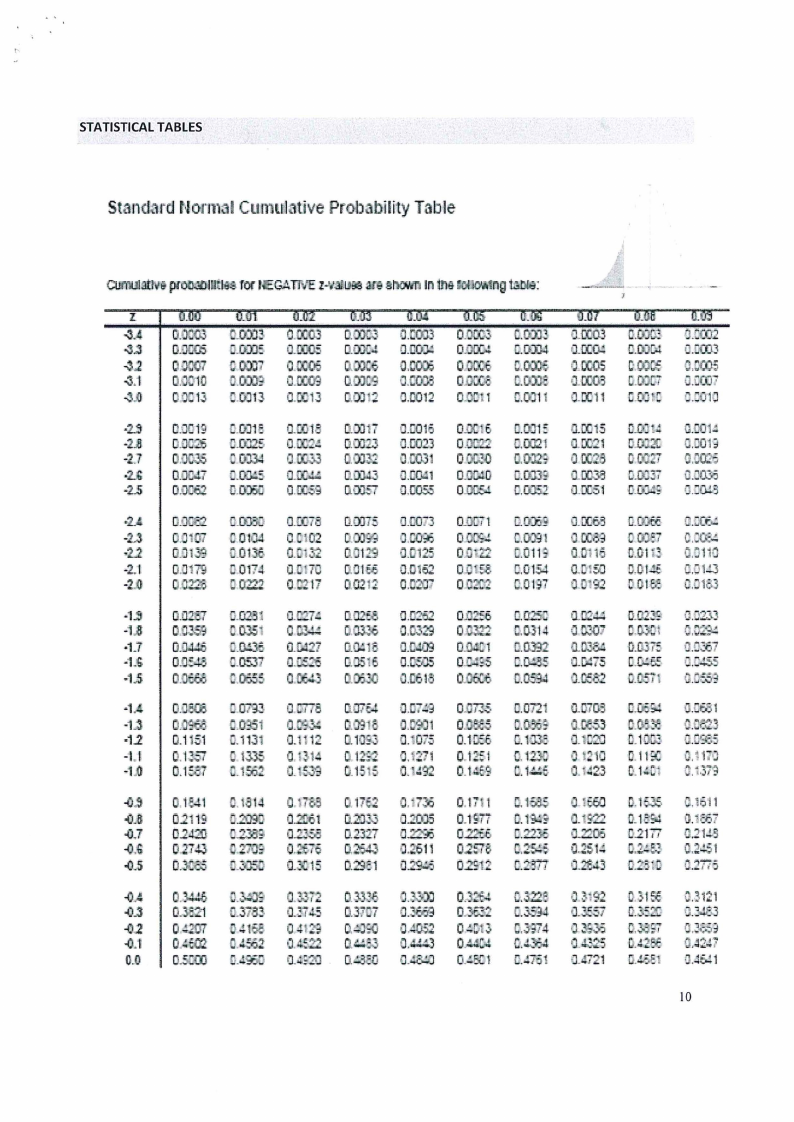
1.10 Page 10 |
▲back to top |
STATISTICALTABLES
S.tanda.rNd orma·C1 u.mll1tive ProbaibmtyTable
cumu1.a·tpr~I .I tort GATin'EZ-'t_,U98 I i!j ·• In~t)t .11n~g4e:
- z.
4_(
-3.3
~2
-3.1
-.,;
.0005
,J.~C•ilS
(l.0012
.OCH
•U
.DJ1:
0.001i .00115
c.001;: C0 .5
·2J8
-2J'
_L0025
" ljl3,:l
m. O.OOiJ _[(r2.'3
,0031
,c.002·1 Q.OOQI
0::12;"IJOC18
·2'
-?.!S
DD,::l5- 0..[('~
GU}J.lJ D.CT~1
..o~o ,J.oc~~O.ii~f .ClOS.5
..00]:
00..';;8
C.00-2 ,JJJ(io·1
lJ..'])48
•2.
-2,3
'
·2-2
·2:11
-2.0
•UI
.o ·7
-l.8
•1J'
4.G
•1.-6
Jg
C011:i.i.
".Ol'"'.
.01?.l.
0222
--~1
OlS
.&3'"
.0...-i.3
iJJ1073
,00""~
,J_C12~
Q_ 1~
0.0@7
C.OJ5_
{,(m
.011~
CJJ15'-t
.01~?'
c.~r:r. Q,
C.0.314 ,J,.,.Xi7
-~ C.039·
Oll~9-5 c..~
0..-· §;fl
-[>!"'I'-
0
C'.Q53..1 .CS.~ "'°i1
•1,4
-·1.3
•1..2
-u
-1.0
.Q7SJ tJITTEI
t035i
- .113
1.:335
-151'6~
0~f27i OJ:£1:
_1J~ 0.1.itf'i4 c.1~~
-0
-tua
-0.7
-0.16
-0.S
f,J. 7t,
t'.!~61
..... ,'?~
~,., 0.17 l C.168.E ~~'j
0.1~1 ,0.1_ 9 -
ii]..:;,._:'
O.nff, C.~. u.2ZDS
0,./76
0 rre C.2S.:~, ,J-2s1..:
O.~lis 0.~~1
o-"'-; t.2'ITT a.2e.i3
Q.2775
-0.A
Cl., it2
•0_3
,1:ir.,;
C.J.22::i
t.3!'J,4
-02
r.14,d
.~•~74
-0.1
tj_4.!22
C.J...~
0.0
•1 _:.J O.~!O
[.JJ\\3
G.4&.l.1
10
|
|
2 Pages 11-20 |
▲back to top |
|
|
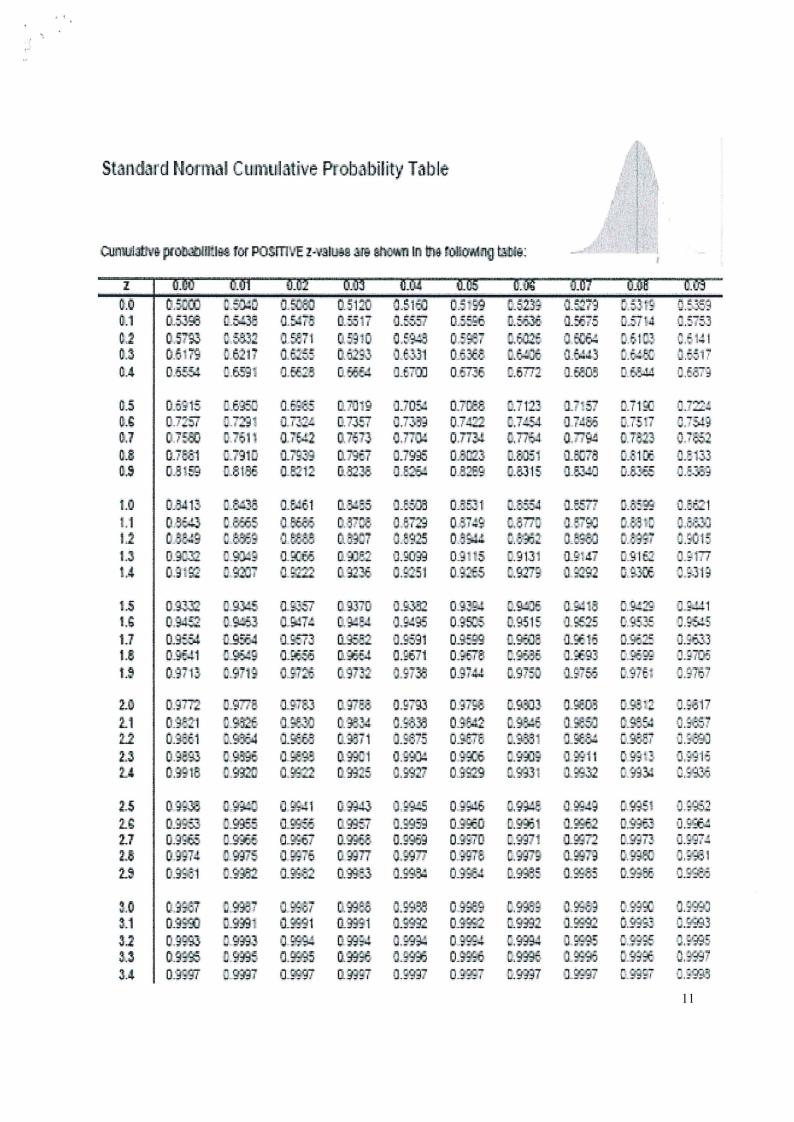
2.1 Page 11 |
▲back to top |
0.0
.1
0.2
0.3
a.~._,;
0,4
0.6eZ~
Ctn'i1S
07i'57
0.-..,
1.0
.1
t2
lJ
A
o.:.r.".' ~-
C(~
-~
119:54 1195§~
ll.%4-1 ~.,
a:r1s .9. 71
(L~67
1::t~U
t].1-7,_
0o-.~;~"'.I ..
a.··.o..! o.r=s c71TI
o.
0.74__
0.1'™
n_. J
0 ~-
O.e.:rnC1._:"li
,e.'S 0 1..,~
.a~~ 0.5;.ll
o.~0!'3
,~_.51
oo..s~55
C.9tl'I
.92i~·
o.s,.,,~
'J,.,-£S5
0.9591
0..JS1
L73S
;c,~~i 0.. 8
.9-$1'5 DSSZS
O.fii1S
2.:5 0..Sl,. !;l;I,;.,; Cl,u~1 0$1'3-Q.
2..S 119~.:-·
oo- 0.!!-'-•M=,. :,11
,u~~ ~;: 'l.1 IJ.9~ S'ItSE, o.~ij? I).~.
2.e Ci.:74
,o.~.75 _ggrr
tl CJ~-!r1 .9~2 aJ:K 033:3
.9"~7
.9~
,.mJ
~:IB-
_9~
Q___,;i; .99~-0
()____1 o.~1~-
,o.w~ 1.1~~4
CL_~5. ll~~
0__97 {1 9,1
.99JE
~-C.9371
L.a~
C.':t~
11
|
|
2.2 Page 12 |
▲back to top |
I'
The t-dishibution
I
,J..-r..-,~_-,._&,~,--_.,.-.,..,.,-I,,Cq.•."-,.<-.O..,A
;r
~- -
.• .,,.,- •• , - - -· - • - •• - , l
· 5~
3:.ml
,7{1
:I
Ii
Ir
l
s jr-
1
I
!II
! ltJ
u
.....
-':'C!
--~--~--~--~-~-«--' 11--~----~---------·~-----------------~----·~----(
13
14
1-
l5
u
17
l!S
19
111)
Y~:r3~
11
•.., -·:':.~lL.:r'b
-·---
l
11
Y---:---,---:-:--@----:--.'.":"'"-,,----,...-------•--,.---·--
HIS j
... J,
12
|
|
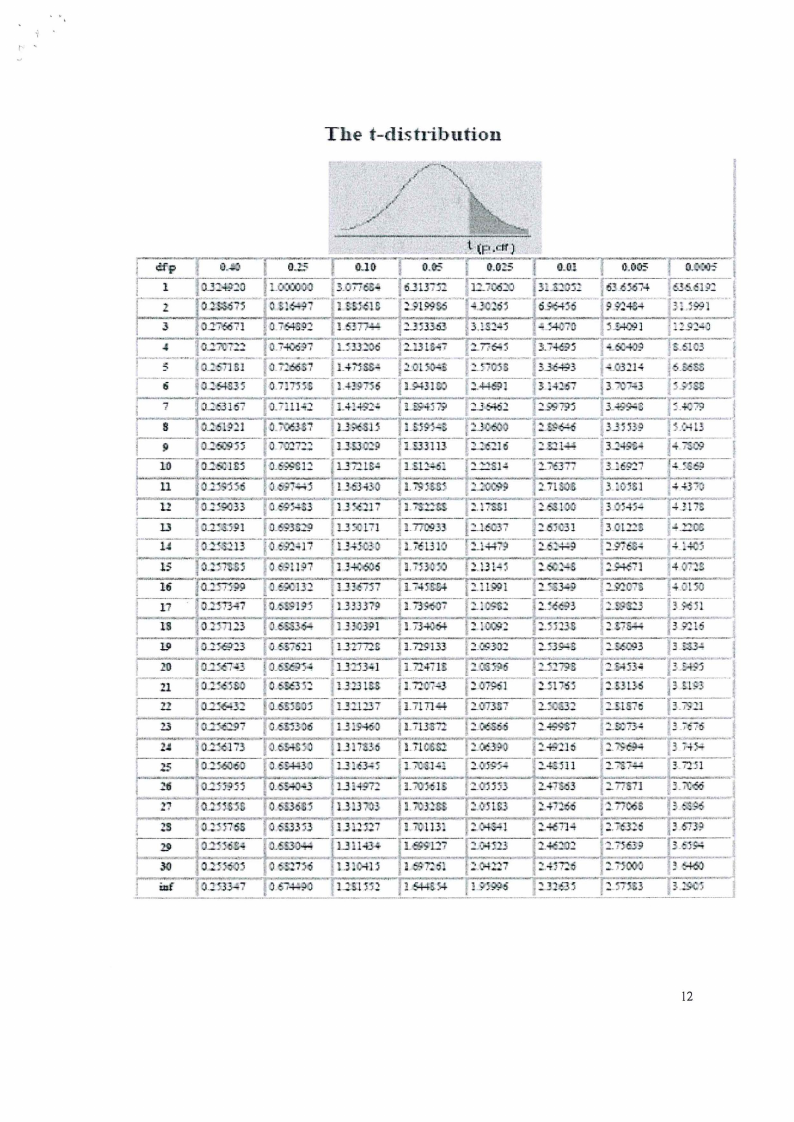
2.3 Page 13 |
▲back to top |
, ''
The Chi-Squat e Distribution
d.1!
)7~ jiCi:,i2
---- ~--- ---- ~---- --~--- ---- -------
~---
'I
I
-r-4---·-~·-,-2:.
13