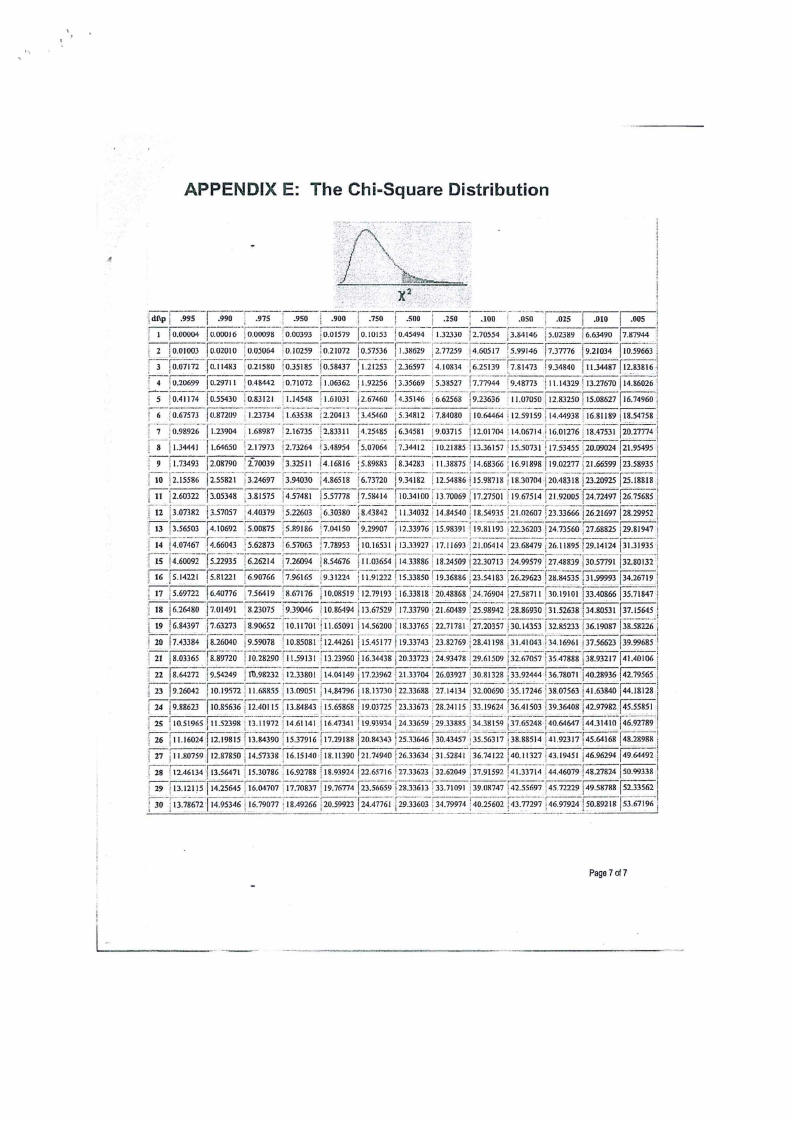
APPENDIX E: The Chi-Square Distribution
..
:··.· ·x~·._, . ,;
I
i I i I i ! i ldl\\p .995
.990
.975
l l .950
.9~~ ·, .750 ;--~00
.250
.100 : .050
.025
!1J0.00004 fo.00016 fo.ooo9s :0.00393 f{J.o1s19 [0.10153 [0.45494 11.32330 jl.70554 IJ.84146 1s.om9 ~j1.s1944
!
2 ~fo.02010
lo.o5o64 _io.10259 _!o.2w12 jo.575J6 _ ~38629 !2.77259_1460511 _!s.99146 ·[urr/6~110.596631
! fJ 0.01112 fo.ii483 10.21580 fo.35185 ·fo.58437 [°imsJ j2.36597 /4.10834 f6.2s139 ?-81473 19.34840 I 11.344s1 fii:'.s3816·!
i i i 4 10.20699 10.29711 0.48442 0.71072 r1.06362 ~2256 !J.35669 rs.38527 , 7.77944 19.48773 1I 1.14329 ~70
114-860261
! f i i I I !5jo.41174 fo.55430 lo.83121 p.14548 1.61031 Jz.67460 '4.35146 6.62568 j9.23636 '11.01oso 12.83250 15.08627 16.74960
i i l 6 /0.67573 ro.87209 : 1.23734 fi.63538 12.20413 f3.45460 ,5.34812 l 7.84080 10.64464 !12.59159 !14.~938 l6.81189118.54758
r 16 i i i : -7 -i 0.98926·-11.·2J904 ; 1.68987- 2.16735--rz.83311-,4.25485 - .34581 ; 9.03715. 12.01704 rl4.06714 16.01276 18.4;53I ;~~-27774
! f I ·j I [- s·•·1··.3j4441 [l.646so (2.11913·• [2.73264.. 3.48954·· 5.01064 7.34412 10.21885 !1J.36157/ 15.50131 f11.s3455 _i20.o<Jo24 21.954;5
I l l 9 jU3493 12.08790 ;2~70039 13.32511 14.16816 /5.89883 jS.3428] j 11.38875 14.68366 16.91898j19.0m7J21.66599123.58935_
r 1 10.. ,2.15586 ·-, 2.55821···13.24697--, 3.94030 ·14.86518--16.73720-·19.34182 ·: 12.54886115.98718 ; 18.30704.120.48318 23.20925 j25.18818
! !11!2.60J22 ·JJ.05348 ~i4.574s1
l5.5ms i1.58414 J10_34100[_13.10069fl1.21501 19.61s14 f21.92oos-J24.12491 l2G.1s6s5
i1"i· 1B:S:ii:isfi.i":oi601·:ii"3366<>-l i:i:011iu-'1is-iiis'i.
t.
(
! ~! i i i ~I 13 j3.56503
! f:i".-:iii'ii;jT522601
!
I
~
. •1.6-:3ois0TsI-::i3s42
1u4on
I
i
I
M.84540
1
1
.
'
t
26.21691 j·'i"s:299.52.
S.00875 5.89186 p.04150 19.29907 jl2.33976 15.98391 \\ 19.81193 22.36203 J24.73560
29.81947'
I ! flo.i6S:llTlm21jl?:11;;;;;- I i-i.·.·14.07467 4.66043 5.62873 J6.57063-;7:-;8953
fii.06414-J23.68479 / 26. l 1895 29.14124 fli31935:
fl's[ r f I ! I f f I ! i 4.60092 5.22935 6.26214 j 7.26094 8.54676 I 1.036S4·114.33886 18.24509 22.30713 24.99579 27.48839 30.57791 32.80132
! 116/s.14221
j5.69ilIl ! ! i : 11
j5.s1221 16.90766 !7,96165 J9.3l224 j11.91222 115.33850 19.36886J23.54183 !26.29623 [2s.84535!3L9~99313~:26719
6.40776 1.s6419 x.67176 110.os519 )12.79193 16.33818 120.48868: 24.769o4121.ss111 fJo.19101 f33.40866135.11847
Gs! I ! ! ! ! i 6.26480 7.01491 8.23075 _,9.39046 I0.86494113.67529 17.33790 21.60489 (25.98942 28.86930 ~j34.80531137.15645
I r i ! !.19 16.84397 j'l.63273 8.90652 Go.11101.' 11.65091 14.56200 j 18.33765 22.71781 fi.1.20357 J 30.14353 32.85233·J36.19087138.58226 I
i 1 20 17.43384 18.26040 19.59078 jl0.85081 12.44261 115.45177r19.33743: 23.82769 128.41198 :31.41043.134.16961 137.56623 139.996851
I j ! jl3.23%0! 21 j8.03365. js.s9120 10.28290 11.59131
! 16.34438!20.33723 i24.9347H j29.61so<1J~2.61os1 !3SA7888 jJS.93211 F40106
I I i I I ! ~! i 22 fs.64272 9.S4249 11l.98232 12.33801 l4.04149 j17.23962 21.33704 26.03927 ; 30.81328
i I 36.78071 40.28936 42.795651
i 1 i , 23 r9.26042 110.19572 , I l.6.~855113.09051 14.84796 118.13730122.33688i 27.14134 32.00690 : 35.17246 38.07563 141.63840144.18128
1241 1 1 r r 1 1 9.88623 J0.85636 112.40115 113.84843__15.65868 19.03725 23.33673 128.24115 133.19624 j36.4l503 39.3r.408 42.97982:145.55851
rzs 1 1 r 12 7 14 \\I0.51965 111.52398 13.11972 14.61141 116.47341 19.93934 4.33659 : 29.3~885:134.38159 13 .6~24~ 140.64647 4.31410J46.92789
r j j26JW6024:!'2'9_815
j n.84390 [ 1~.37916!11.291s8120.84343 25.33646 j3Q.43457_!35.5631713s.88514 l41.9231: 14s.~16s [\\s.28988
1 27 11.80759_112.87850 114.57338 116.15140·: I8.11390 121.74940126.33634 31.5284I 136.74122 :40.11327 143.19451 146.96294 149.644921
~~4'~~-30786
iIG.92788 j18.93924_jll.6S7l6 !.27.33623~!37.91592
~3714f44.46079148.27824_~!,
I i ! I j 29 IJ.1211s j 14.25645 j 16.04707 17.70837 19.76774 j23.566S9 j2B.33613 !33.71091 [39.oS747 J42.55697 j4s.12229!49.58788152.33562
i fw.mi} ! 30 /13.78672·114.95346116.79077 rl8.49266
j24.47761 29.33603 !34.79974/40.25602 143._77297i46.97924·jso.89218153.67196
Page7 of7