 |
AEM702S - APPLIED ECONOMETRIC MODELLING - 2ND OPP - JAN 2023 |
 |
1 Page 1 |
▲back to top |

nAmlBIA unlVERSITY
OF SCIEnCE Ano TECHnOLOGY
FACULTYOF HEALTH,NATURALRESOURCESAND APPLIEDSCIENCES
DEPARTMENT OF MATHEMATICS AND STATISTICS
QUALIFICATION: Bachelorof Sciencein Applied Mathematics and Statistics
QUALIFICATION CODE: 07BSAM
LEVEL: 7
COURSE CODE: AEM702S
COURSE NAME: Applied Econometric Modelling
SESSION: January, 2023.
DURATION: 3 HOURS
PAPER:THEORY
MARKS: 100
SECONDOPPORTUNITY/SUPPLEMENTARYEXAMINATION QUESTION PAPER
EXAMINER
Prof. RakeshKumar
MODERATOR:
Prof. Peter Njuho
INSTRUCTIONS
1. Answer ALL the questions in the booklet provided.
2. Show clearly all the steps used in the calculations.
3. All written work must be done in blue or black ink and sketches must
be done in pencil.
PERMISSIBLEMATERIALS
1. Non-programmable calculator without a cover.
2. Statistical tables will be provided when needed.
THIS QUESTION PAPER CONSISTS OF 3 PAGES (Including this front page)
 |
2 Page 2 |
▲back to top |

Question 1. [Total Marks: 20]
Given the following information on dependent variable Y and two independent variables X2
and X3:
Number of observations, n=15.
Y- = 1942.33, -X2 = 2126.33, X- 3 = 8.0, IC~- Y-2) = 830121.33,
xx= l 15
[
31895
120
31895
68922.513
272144
120
272144
1240
l ky =
29135
[ 62905821
247934
37.2324 -0.0225
l (xX)-
1=
[
-0.0225
1.3367
0.00001
-0.0008
1.3367
-0.0008
0.0540
y'y = 57,420
p Residual Sum of Squares (RSS),I u/ = y'y- Xy =1976.8557
Explained Sum of Squares (ESS)=828144.4778
Total Sum of Squares (TSS)= 830121.333
Answer the following questions:
(a) Find p.
(b) Fit the regression model of Yon X2and X3.
(c) Find R2 .
(d) Develop ANOVA table and test the hypothesis H0 : {32 = {33 = 0.
(6 marks)
(4 marks)
(4marks)
(6 marks)
Question 2. [Total Marks: 20]
(a) Prove that in a classical linear regression model, OLSestimators have minimum variance.
(10 marks)
(b) How can the problem of heteroskedasticity be removed by the method of generalized
least squares?
(10 marks)
Question 3. [Total Marks: 20]
(a) Discuss the estimation of parameters of a regression model in presence of perfect
multicollinearity.
(10 marks)
(b) Using matrix approach, prove that in a multiple regression model, the OLSestimators are
unbiased.
(10 marks)
2
 |
3 Page 3 |
▲back to top |
Question 4. [Total Marks: 20]
{a) List the assumptions of classical linear regression model.
(b) What is identification problem?
{b) Discussthe Koyck's approach to distributed lag models.
{6 marks)
(4 marks)
(10 marks)
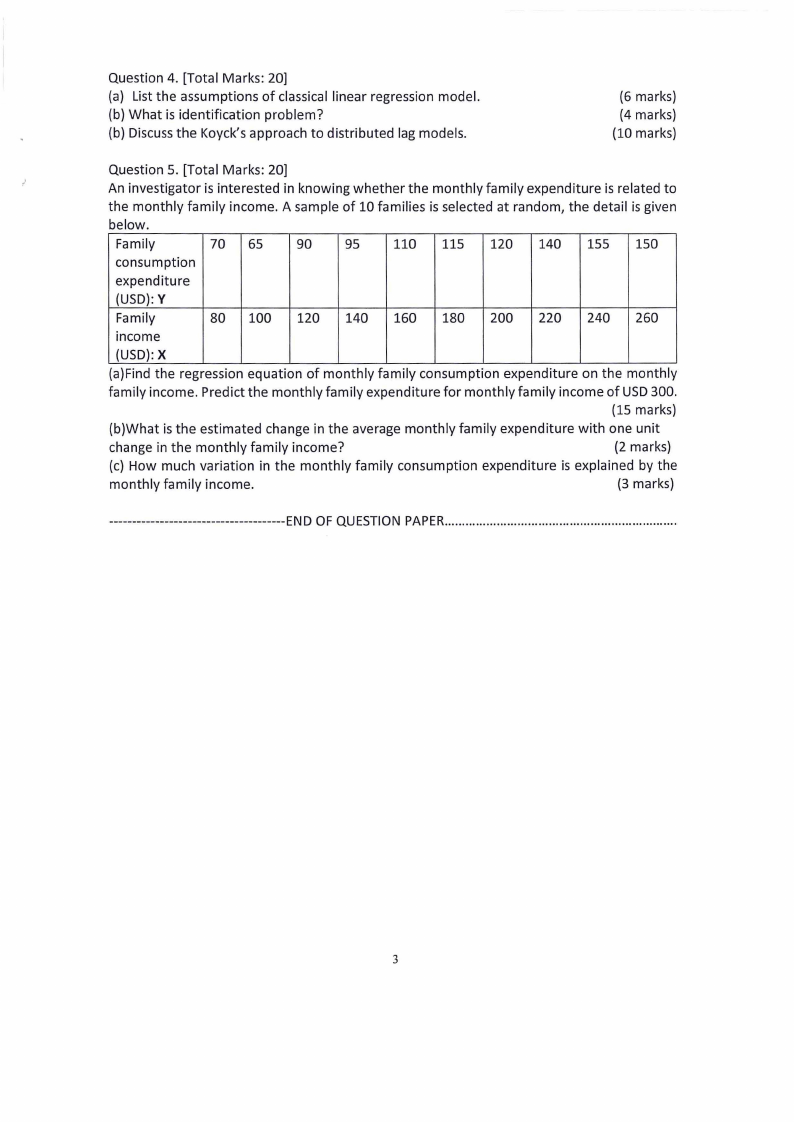
Question 5. [Total Marks: 20]
An investigator is interested in knowing whether the monthly family expenditure is related to
the monthly family income. A sample of 10 families is selected at random, the detail is given
below.
Family
70 65 90 95 110 115 120 140 155 150
consumption
expenditure
{USD):Y
Family
80 100 120 140 160 180 200 220 240 260
income
{USD):X
(a)Find the regression equation of monthly family consumption expenditure on the monthly
family income. Predict the monthly family expenditure for monthly family income of USD300.
(15 marks)
{b)What is the estimated change in the average monthly family expenditure with one unit
change in the monthly family income?
{2 marks)
(c) How much variation in the monthly family consumption expenditure is explained by the
monthly family income.
{3 marks)
--------------------------------------END OF QUESTIONPAPER..................................................................
3





