 |
SIN601S - STATISTICAL INFERENCE 2 - 2ND OPP - JANUARY 2024 |
 |
1 Page 1 |
▲back to top |

nAmlBIA UntVERSITY
OF SCIEnCE AnDTECHnOLOGY
FacultyofHealth,Natural
ResourceasndApplied
Sciences
Schoolof NaturalandApplied
Sciences
Departmentof Mathematics,
Statisticsand ActuarialScience
13JacksonKaujeuaStreet
PrivateBag13388
Windhoek
NAMIBIA
T: •264 612072913
E: msas@nust.na
W: www.nust.na
QUALIFICATION: Bachelor of science in Applied Mathematics and Statistics
QUALIFICATION CODE: 07BSAM
LEVEL: 6
COURSE CODE: SIN601S
COURSE NAME: STATISTICALINFERENCE2
SESSION: JANUARY 2024
DURATION: 3 HOURS
PAPER: THEORY
MARKS: 100
SUPPLEMENTARY/ SECOND OPPORTUNITY EXAMINATION QUESTION PAPER
EXAMINER
Dr D. B. GEMECHU
MODERATOR:
Dr D. NTIRAMPEBA
INSTRUCTIONS
1. There are 5 questions, answer ALL the questions by showing all the necessary steps.
2. Write clearly and neatly.
3. Number the answers clearly.
4. Round your answers to at least four decimal places, if applicable.
PERMISSIBLE MATERIALS
1. Nonprogrammable scientific calculators with no cover.
THIS QUESTION PAPERCONSISTSOF 3 PAGES(including this front page) and 4 EXTRA
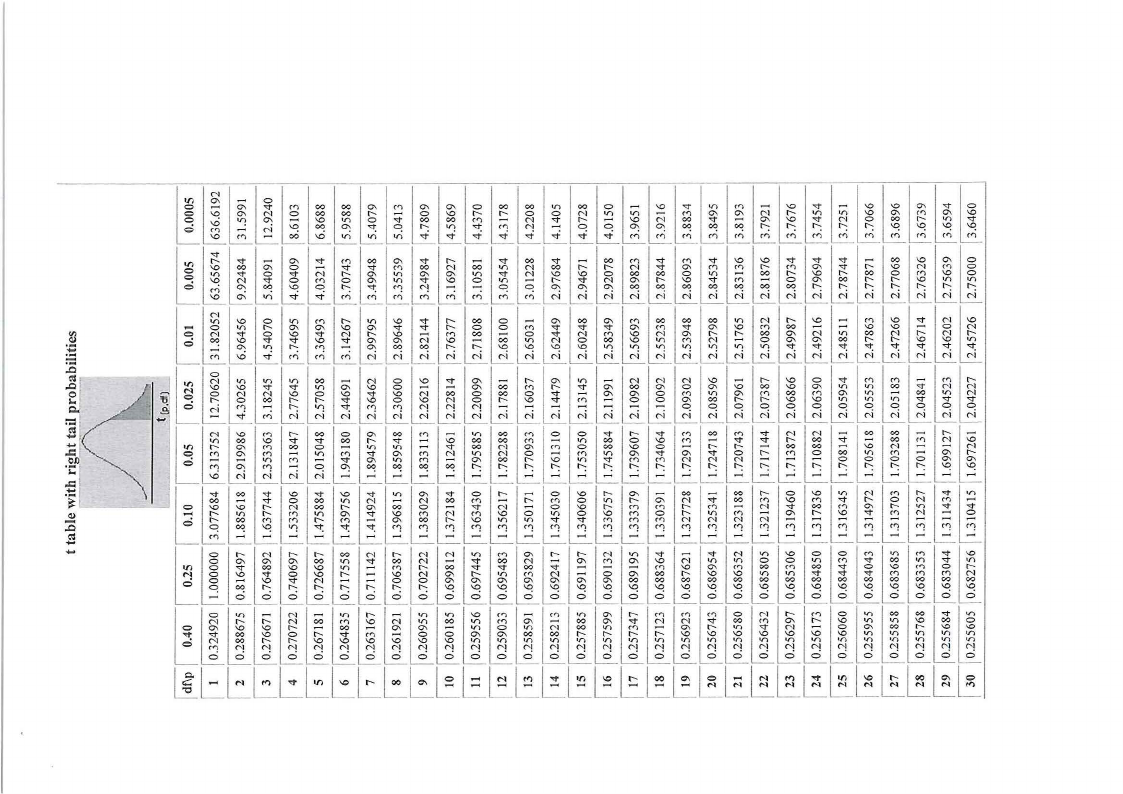
x ATTACHED STATISTICAL TABLES (Z-, t-, 2- and F-distribution tables)
 |
2 Page 2 |
▲back to top |

Question 1 (24 marks)
1. Suppose the random variables Xi, X2, .•., X7 are independently and identically distributed
exponentially with the parameter A = 1, that is
Xt > 0
elsewhere
Let Y1 < Y2 < ... < Y7 be the order statistics for Xi, X2, ... , X7 . Then,
1.1.The pdfofthe r th order statistics.
rs)
1.2.The pdf of the minimum order statistics, Y1. Which density function does the pdf of Y1 belongs
to?
141
1.3.The pdf of the maximum order statistics
13)
1.4.The pdfofthe median
13)
1.5.The joint pdf Y1 , Y2 , ... , Y7
14)
1.6.The joint pdf of the 2nd and 7th order statistics
15)
Hint:
!Yi, = v/Yt, yJ (i-1)!0-~~l)!(n-J)!
[F(yt)]i-1 f(yt) [F(yi) - F(yt) ]1-i-1 f(YJ )[ 1 -
F(Y1)r-J.
= fyr(y) (n-r)~~r-l)! [Fx(y)JT- 1 [1- Fx(y)]n-rfx(y).
Question 2 (21 marks)
2. Let X11X2 , .... Xn be independently and identically distributed with normal distribution having
E(Xi) = µ and V(Xi) = cr2 •
2.1. Show, using the moment generating function, that X= I1=2xi has a normal distribution with
n
cr2
_!. 2 z
mean µx =µand variance cr~=-;;--(Hint: use Mx1(t) = eµc+zcrt ).
[8]
2.2. If is a 2 assumed to be known, derive the 100(1 - a)% Cl forµ using the pivotal quantity
method.
[S]
2.3. If n = 9 and a 2 = 16, then find the value of k such that
~x = 2.3.1. P(S 2 :5 k)
0.05. Hint: (n-
l)
sz
2(1
2 (n-1)
[4)
C';µ) k) 2.3.2. P (Lf=l
2
:5
= 0.25
[4]
Question 3 (26 marks)
3.1. Consider a random variable X with the probability distribution given in table below with
unknow parameter 0:
X
P(x)
20/3
I ~(1-8)/3
I ~1-8)/3
Find the estimator of 0 using the method of moment estimation technique.
[S]
Page1 of 2
 |
3 Page 3 |
▲back to top |

3.2. Let Xi, X2, X3 , X4 be a random sample from a distribution with density function
1--¥ f(xdfJ) = Pe
{0,
, for xi> 4
otherwise
where fJ > 0.
3.2.1. Find the maximum likelihood estimator of fJ
[6]
3.2.2. If the data from this random sample are 8. 2, 9.1, 10.6 and 4.9, respectively, what is the
maximum likelihood estimate of {3?
[3]
= 3.3. Observations Y1 , ... , Ynare assumed to come from a model with£(~)
2 + 0xi where
0 is an unknown parameter and Xi, x2 , ... , Xn are given constants. What is the least square
estimator of the parameter 0?
[6]
3.4. Supposethat£(0 1 ) = E(0 2 ) = 0, Var(0 1) = crfand Var(0 2) = crl,Furthermore, consider
= that 03 a0 1 + (1 - a)0 2, where a is any constant number. Then,
3.4.1. Show that 03 is unbiased estimator for 0
[2]
3.4.2. Find the efficiency of 01 relative to 03
(4]
Question 4 [9 marks)
4. Let X1,X2,..., Xnbe an independent Bernoulli random variables with probability of success 0 and
probability mass function
= f(xd0)
0X1(l - 0)l-X£
{ 0,
'
for X; = 0, 1
otherw•ise
Suppose 0 has a beta prior distribution with the parameters a and {3, with probability density
function
for O < 0 < l; a> 0 and {3 > 0
If the squared error loss function is used, show that the Bayes' estimator of 0 is given by
Ll~,qx,+a
a+P+n ·
= Hint: lfY~Beta(a,{3), then E(Y) a+ap·
[9]
Question 5 [20 marks)
5. Let Xi,X 2, ••• , Xn be a random sample from the exponential distribution with the parameter 0
and the probability density function xi is given by
for Xi> 0
otherwise
5.1. Show that the mean and variance of Xi are¼ and 0\\, respectively.
[6]
Hint: Mx,(t) = (e~t)
5.2. Show that the Xis a minimum variance unbiased estimator (MVUE)of¼-
[10]
5.3. Show that X is also a consistent estimator of¼-
[4)
Page 2 of2
 |
4 Page 4 |
▲back to top |

l!lili[lililllllll[lilll[li nli~llli~~lllllilili[li[llliltllll •
-
N•
M 00 N M -
-
•
•
MO
-
-
M
00 00
M
-
00 N
00 -
M
00 0
-
M•
00 00 00
99
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
l!lili[~lllllilll[~lillll~ltlilllilllllili[lllllilllill~li~llllll -
-
M
0
-
•00
•
00
-
-
N
00
O
-
M
-
00
-
0
N
M•
MN
ci 6 ci ci ci
ci 6 ci ci ci d d d d d
-
00 -
M
00 00
00 00 00
d d dd dd ddd d
l!lilillll~ll~li[l!_U_ill_l!_l!_lilllilillll~lilllilllililllllillllll •
0
00
N
0
•
00 -
•
ci ci ci ci
•
00 •
-
N
-
0
00 -
M•
00 00
0
M
-
N
•
00 00 00
6 d d ci 6 ci ci 6 d d ci ci ci 6 ci ci ci ci ci d d
l!lililill[~lllllilllil[ll[lllll[lllllill ~lllilllillllltllllll M
M
N
O
N
-
M
0
-
0
00
0
•
00 0
M•
00 00
N
0
•
-
•
0
M
-
N
•
00 00 00
ci ci ci ci ci d d ci ci ci ci d ci ci d 6 6 ci 6 6 6 ci 6 6 6 6 ci ci 6 6 6
]
QN
l!lillllll[li[lilll[[li[~llltlllllllll!_lilll!_lilllllilillll 00
00 N •
M
-
g
= i•
•
00 •
00 N 00
0
0
00 •
i
N
9o
o9
9
O
o
o
o
O
O
O
O
O
O
O
O
O
O
O
O
O
O
O
O
O
O
O
O
O
OO
O
O
r
0
l!lili~lt[~W_llll~llli[lllililllililili~lllllllllllilllillll ~. •~~•MO
00 0
N 0
N
00
M
M
0 N.
00 00
0
-
M
0
M
N
0
N
M•
00 00
999
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
,
l!lililill~~~li~~lilillllllllllllllllll[lilililllinli~lilllill~ll M N -
-
-
M 00 0
0
00 M
00 00
M 00 M
0
N
•
00 00
0
-
N
0
M
N
•
0
N
M
•
00 00
999
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
l!llllli[lll!_~lilll,[~~lllililllllllilllilllllilllilllillll 00
0
•
N 00 N •
00 N
M
ci ci
M-
00 00
N
N
00 M
N
•
00 00
N
•
00 0
N
M
•
00 00 00
ci ci ci ci 6 ci d d d d d ci d ci ci ci ci ci ci d ci
l!ll09~li9• '~090li'N~[-[-li~N ll-li-U- _-• U_o00ol0 [,~N l!M_~• l!_~ll•l!_~00[•0l0l~00ll•l!_•~-l[~liNll•ll~l!_N~•[~l!_~l!_~l
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
l!l!lil!_lili~lili[[ll ~li~l!_lllllilllilili~lillllll~lllill~lllillll 0
-
00 00
-
•
M
M
-
N
-
M
00 00
90 M9 9 -
N
00 -
00 0
-
M•
00 00 00
0
0
00
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
 |
5 Page 5 |
▲back to top |
l! lll_[i_-_-~[_--ll-[l-1-li~[llli[~l~i~li[~ll~l1-~--li[ °' - -
C\\
0v
\\\\N.00
C,,\\.,
N
C\\
M
\\0
<ri
-
M 00 00 C\\
M C\\
C\\
0
00 00 V)
O 00 00
-
\\.0
,,.,
0
-v
0
\\.0
00 00 <'l -
0
N
0v
\\.0
00 C\\
V
O
V)
V
M
N
-
00
If) V) V)
00 0
N
V-)
0
0
-
\\.0
V
V)
M-
V)
\\.0
-
N
M
C<:>
Cv \\
C-\\
N
0\\
C\\ C\\ 00 00 00
M <f'l M ,,.;
r')
\\.0
V
-
V)
,,.,
\\.0
V
N
c-ri M cf)
\\.0
\\.0
C\\
V0
\\.0
O
C\\
M
0\\
C<:>
V)
\\v.0
\\.0
\\.0
\\.0
\\.0
,...; ,r; rri cf') r'1
~[l!l!lllilll! l!lil!l!lill[li~l!l!li~l!l!l!llli[~li \\.0
0V 0
-
C\\
C0 \\
-V
M• 0• 0 MC\\
0V0 N
0- 0
•
V)
0N0 0• 0 -
00 MN ••
M
C\\
M•
M\\.0
\\.0
M•
•
C\\
•
•
-
C<:>
\\.0
\\N.0
MC\\ 00
C\\
00 \\.0 0
8v M N
-
-
0
R.
8
O C\\ C\\ C\\ 00 00 00 00 00 00 00
R
'°
V)
\\.0
0
V)
M
V)
\\.0
•
00 0
-
C\\
00 C\\
M
00 00 00 V)
N
\\.0
-
M
\\.0
•
N
\\.0
0
V)
C\\
0\\
\\.0
C\\
•
•
0 0 M•
•
V C\\ M •
C\\
\\.0
M
00 -
-
\\.0
\\.0
-
0N
-
N•
0
00 \\.0
•
\\v.0
v
\\.0
Nv
C\\
\\.0
0\\
-
N
M 00 -
O•
\\.0
-
00 V)
N
N
M
\\.0
N
C\\
O
00 \\.0
V)
M
N
-
00 0\\
N
V)
00 N
N
0
C\\
C\\
00
\\.0
\\.0
,,.,
;
C\\
,,.,
M-
C\\ 00 00
\\.0
\\.0
\\.0
\\.0
V)
V)
V)
V)
V)
V)
V)
V
V
V
V
V
V
VV
-~1- /1 0,_,
-]=i,c--' [°' [- l!•[,,[.,.[.,N [~[,[.,.l,!.[°,v['°'[v11[~-[Mlio[oo l!- 1·c;' '~
1 Ir)
N
,,., V)
V) 00 -
N
O
\\.0
"<:I" C\\
-
C\\
V)
-
N
N
N
\\.0
-
\\.0
0
V <'°l M -
f'°l
S \\O.0
vi
•
N0\\.0
V0N0
v
\\0
V0 )
0\\
\\v.0
\\V.0
\\.0
0
\\0.0
N-
\\.0
0N- 0
C0 O \\
0000
<0 '°l
\\.0
vV
,v-,-,
0\\
C- \\
00
C0 \\
Co 0 \\
OM
0\\
C\\
V00)
\\0
C\\
0M 0
\\0.00
CM \\
V)
0\\
\\.0
\\.0
V)
V)
,,.,
V)
00
-
•I)
• 0v 0
N
VV )
NVN
&0
M-
V) V M M N N N -
-
-
-
-
-
-
O O O O O O O O O O O0
.o'
;
"' · ~10/'l ~,.-.,
-
\\.0
N
; ;;;: ;
;
V")' M-: ll-,,.[,"V-;:;C\\ V) M -
N
N
N
-
-
-
-
-
;;;;;;;;
;;
;;
;
0r\\-: 0r0-: r-: r\\0-: rV)-: rV-: rM-: Mr-: rN-: rN-: Nr-: r- -: r- -: r- -: 0r-: l!r0,-,:.,r0-: [-r0-: 0\\ ~Cr\\-2
"::___---=- - - - - - - - - - - - - - - - - -
>
oo -
v
O 00 V) N
-
N 00 M -
M
O
V)
C\\ N V 00 M \\.0 M V
0 N M-
-.l:l
~[l |
6 Page 6 |
▲back to top |

---
~llll"llll[lllllrl,ll"ltlMl"lMlllMl!lMll.l.ll.l.l~lillll'l •
'-0
-
C-1 '-0
M
-
00
•
M
M
-
••
N
00
0
'-0
N
00
00
M
'-0
•
'-0
00
0
•
00 '-0
-
00 '-0
N
'-0
-
-
00
•
M
-
M
'-0
•
•
00
00
-
-
0
'-0
-
00
0
00
N
00
•
M
00
00
6
0
N
6
,r, -
0
NN
00
M
C00-I N
-
'-0
•
-
0
N
'-0
O6O MN
'-0
-
-
-
-
-
NNNNNNN
M
M
M
V•
•
~~~l~~~~l~"!'l°llll~lM~lll!~'~llllil 0
-.::t"
M
•
'-0
•M
0-
M•
N
'-0
-
-
N
MN
'-0
-
0
0O 0
0- 0
V
O
0
6
-
-
-
N
O'\\
C"'I O'\\
V
'-0
Noo
N-
'-0
'-0
0N
N
N-
00
•
'-0
-
0
NNNNNN
O'\\ °'
M 00 N
-
MV
00
0
'-0 N
00
0
•
00 0
-
'-0
M
N00
M
'-0
6
0
6
MM MM MM M•
•
•
-
N
00 -
•
-
N
00
N
M-
•
'-0
'-0
N
00
00
0
6
•
•
•
•
•
~ll[lll!~lllll!llll[ll_~lllill[OOMlllllll!lllilt[lilili m
0
N
M
t"--
r--- -
0
MM
O
M
M
00 r---
0
-.:t -
r--- N N
00
•
MN
N•
N M O '-0
00
00
-
'-0 N
00 0
•
'-0 M •
0
N
M
00
•
M
•
-
M
N
00
N
M
M
-
00
•
N
'-0
00
'-0
•
N
'-0 N
N
•
-
00
•
0
0
•
M
-
•
00
-
00
-
•
0
M '-0
-
•
O
M
1~
t"-- O'\\
.,....
-
-
0
-
-
-
6
C"'I <"'I
0
C"'I C"'I C"'I C"'I C"'t
6
rf"l
...:2._ t<"\\
cri
M
0
M
M
M
6
0
-.:t "'1'" -.::t" -.::t" -.:t "'1'"
~~~~~!l[lll[[[Ml |
7 Page 7 |
▲back to top |
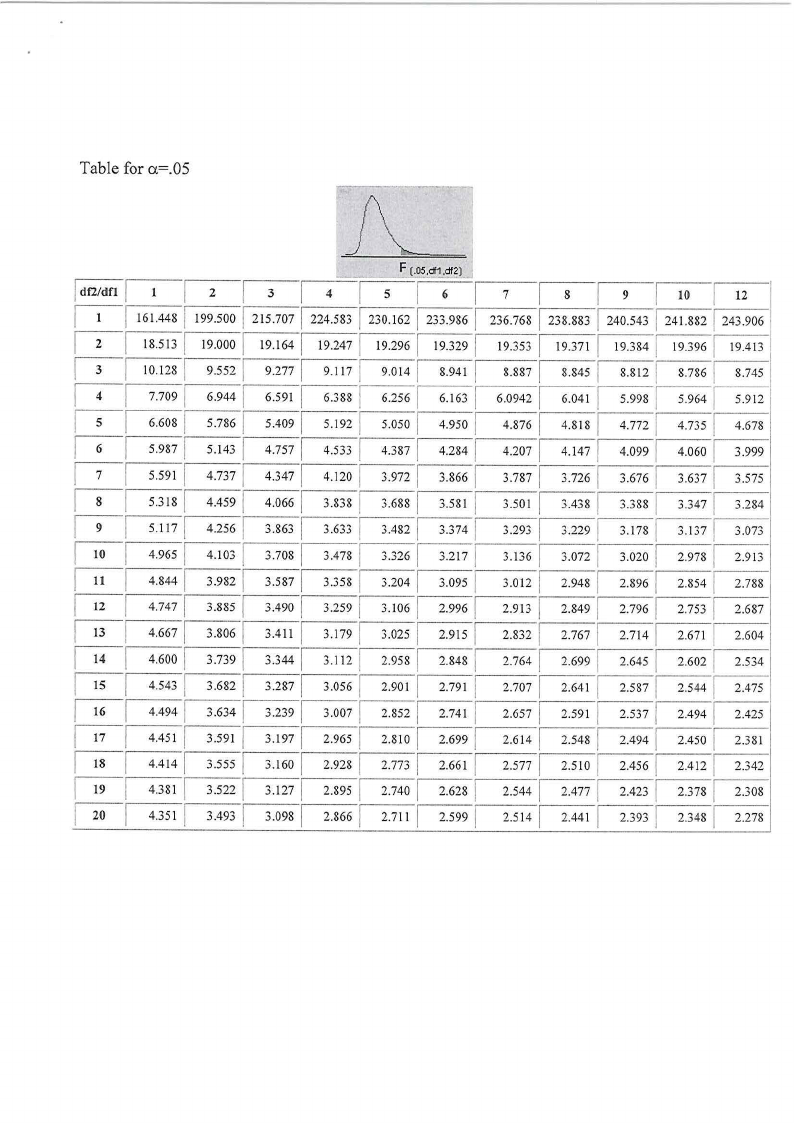
Table for a=.05
Idf2/dfl
Il
I2
I3
I4
I5
I6
I7
I8
I9
I 10
I 11
I 12
I 13
I 14
I 15
I 16
I 17
I 18
I 19
F (.os,df1,di~ J
I I 1 I 2
3
I 161.4481 199.500 1 215.707
4
224.583
I 5
6
I7
I8
I 230.1621 233.9861 236.768 238.883
I 18.5131 19.ooo 1 19.164
I 10.128 9.5521 9.277
19.247
9.117
19.296 1 19.3291 19.353 1 19.371
9.0141 8.941 1 8.8871 8.845
I 7.7091 6.944 6.591
6.388
6.2561 6.163 1 6.09421 6.041
6.6081
5.9871
I 5.591
I 5.318
I 5.111
5.7861
I 5.143
4.7371
4.4591
4.2561
5.409
4.757
4.347
4.066
3.863
5.192 5.050
4.533 4.387
4.120 3.972
3.8381 3.688
3.633 I 3.482
I 4.950
4.2841
3.8661
3.581 1
I 3.374
4.8761 4.818
4.2071 4.147
3.7871 3.726
I 3.501 3.438
3.293 1 3.229
4.9651
4.8441
4.103 1 3.708
3.9821 3.587
3.478 I 3.326
I 3.358 3.204
3.211 1
3.0951
I 3.136
I 3.012
3.072
2.948
I 4.7471
4.6671
3.885 1
3.8061
3.490
I 3.41 I
3.2591
3.1791
I 4.600
3.7391 3.344
3.1121
3.106
3.025
2.958
2.9961
2.915 1
2.8481
2.913 1 2.849
2.8321 2.7671
2.764 2.699
4.543 1 3.6821 3.287
4.4941
4.451 1
4.414 1
3.6341
3.59 I I
I 3.555
3.239
3.197
3.160
4.381 1 3.5221 3.127
3.0561 2.90.1
3.001 I 2.852
2.9651 2.810
2.9281 2.773
2.895 1 2.740
2.791 1
2.741 1
2.6991
2.661 1
I 2.628
2.707
2.657
2.614
2.577
2.544
2.641
2.591
2.548
2.510
2.477
I I 9
10
12
I 240.543 241.882 243.906
19.384 1 19.396 19.413
8.812 1 8.786 8.745
5.998 5.964 5.912
4.772 4.735 4.678
4.099 4.060 3.999
3.676 3.637 3.575
3.388 3.347 3.284
3.178 3.137 3.073
3.020 2.978 2.913
2.896 2.854 2.788
2.796 2.753 2.687
2.714 2.671 2.604
2.645 2.602 2.534
2.587 2.544 2.475
2.537 2.494 2.425
2.494 2.450 2.381
2.456 2.412 2.342
2.423 2.378 2.308
I 20
4.351 1 3.493 1 3.098
2.8661 2.711
2.5991
2.514
2.441
2.393
2.348
2.278





