 |
MAP602S - MATHEMATICAL PROGRAMMING - 1ST OPP - NOV 2022 |
 |
1 Page 1 |
▲back to top |

r
nAmlBIA unlVERSITY
OF SCIEnCE AnD TECHnOLOGY
FACULTYOF HEALTHAND APPLIEDSCIENCES
DEPARTMENTOF MATHEMATICSAND STATISTICS
QUALIFICATION: Bachelor of science in Applied Mathematics and Statistics
QUALIFICATION CODE: 07BSAM
LEVEL: 6
COURSECODE: MAP602S
COURSENAME: MATHEMATICAL PROGRAMMING
SESSION:NOVEMBER 2022
DURATION: 3 HOURS
PAPER:THEORY
MARKS: 100
EXAMINERS
MODERATOR:
FIRSTOPPORTUNITYQUESTION PAPER
MR. B.E OBABUEKI, MR J AMUNYELA
PROFESSORADETAYO EEGUNJOBI
INSTRUCTIONS
l. Answer ALL questions in the booklet provided.
2. Show clearly all the steps used in the calculations.
3. All written work must be done in blue or black ink and sketches must
be done in pencil.
PERMISSIBLEMATERIALS
1. Non-programmable calculator without a cover.
THIS QUESTION PAPERCONSISTSOF 3 PAGES(Excluding this front page)
 |
2 Page 2 |
▲back to top |

(
Question 1 (10 marks)
A cobbler makes three types of shoes: stiletto, casual and park. Each pair of stiletto takes 8
hours to fabricate, 5 hours to sand and 6 hours to couple. Each pair of casual takes 6 hours to
fabricate, 4 hours to sand and 2 hours to couple. Each pair of park requires 5 hours of
fabrication, 2 hours of sanding and 4 hours of coupling. The cobbler has 96 hours for
fabrication, 44 hours for sanding and 58 hours for coupling. The profit margins are N$38 per
pair of stiletto, N$26 per pair of casual and N$22 per pair of park. Model this information into a
linear programming problem. Declare your variables unambiguously and name the constraints.
DO NO SOLVE.
(10}
Question 2 (13 marks)
Solve the following linear programming model graphically:
Minimize H = I Sa+ l 2b
Subject to 6a + 6b 36
3a+9b 27
b~3
a~IO
a; b 0
Use 1cm to I unit for each of the axes.
(13}
Question 3 (28 marks)
Consider the following L-P model:
Minimize C = 40a + 60b + 48d
Subject to 5a + 3b + 4d 7
2a + l 2b + 8d 21
a~O;b ~O;d~O
3.1 Write down the dual of the model.
(6)
3.2 Solve the dual model.
(13}
3.3 Suppose the solution of the dual model is x =4; y =4; t, = 12; t2 = 0; t3 =0; C =112.
Use this solution to determine the solution ofthe given primal model.
(9}
Page 1 of 3
 |
3 Page 3 |
▲back to top |

Question 4 (18 marks)
Consider the following L-P model:
Minimize Q =2x+4y+5z+3t
Subject to -x-2y+2z
~40
3x +2z+t:::; 100
X -2y -z+4t~50
x;y;z;t 0
4.1 Identify all the non-basic variables in the model.
4.2 Express H = A1 + A3 in terms of the non-basic variables.
4.3 Write down the initial tableau for the phase 1 of the two-phase method.
4.4 Given that the final tableau of phase 1 is
X
y
z
t
s1
s2
s3
Al
A3
H
-1
-2
2
0
-1
0
0
1
0
0
31
22
0
0
9
8
2
-9
-2
0
1
-6
0
8
-1
0
-2
1
2
0
0
0
0
0
0
0
0
-1
-1
1
(3)
(3)
(4)
40
340
140
0
and that the original objective function is expressed in terms of non-basic variables for
phase 2 as 8Q = 33x+ 90y+ 23s1 +3s 3 + 1220, determine the solution of the given L-P
model.
(8)
Question 5 {20 marks)
Consider the following transportation table:
Destination 1 Destination 2 Destination 3 Destination 4
Source 1
10
8
20
11
Source 2
12
9
7
20
Source 3
6
14
16
18
Demand
10
15
15
20
Supply
20
25
15
5.1 Determine the initial transportation cost using the Least-cost method.
(8)
Page 2 of 3
 |
4 Page 4 |
▲back to top |
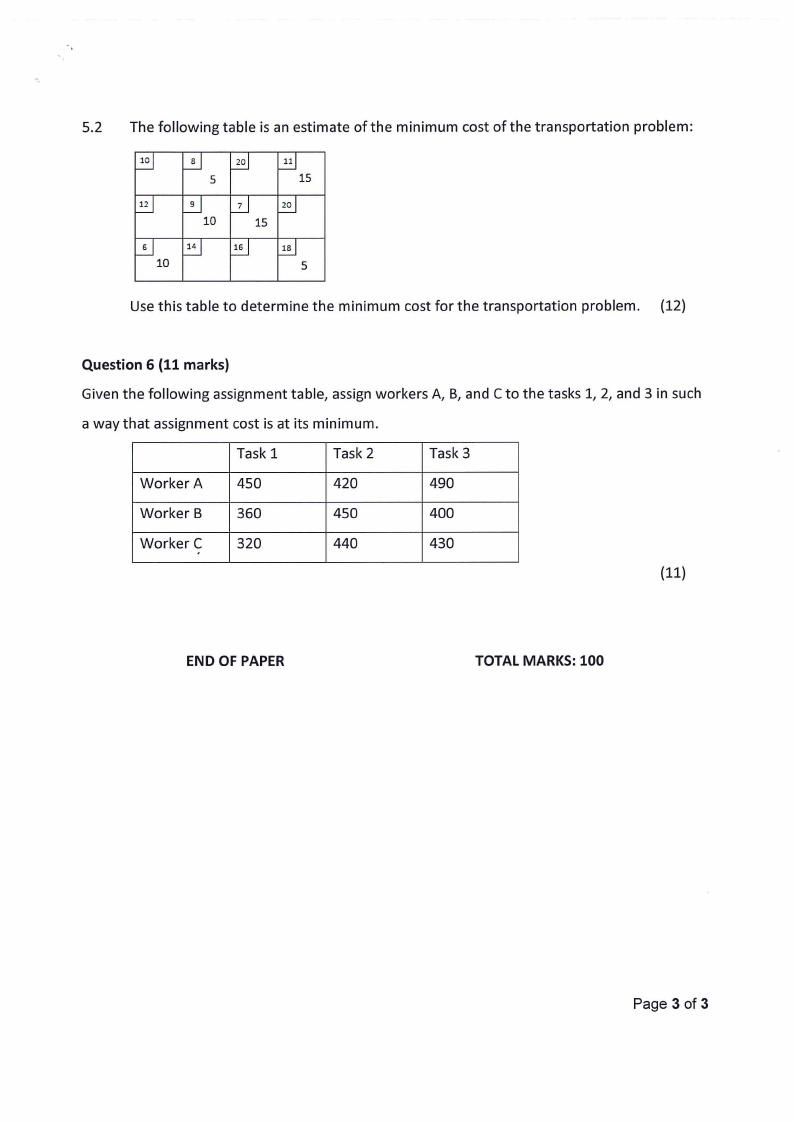
5.2 The following table is an estimate of the minimum cost of the transportation problem:
10
B
20
11
5
15
12
6
10
5
Use this table to determine the minimum cost for the transportation problem. {12)
Question 6 (11 marks)
Given the following assignment table, assign workers A, B, and C to the tasks 1, 2, and 3 in such
a way that assignment cost is at its minimum.
Task 1
Task 2
Task 3
Worker A 450
420
490
Worker B 360
450
400
Worker C 320
440
430
{11)
END OF PAPER
TOTAL MARKS: 100
Page 3 of 3





