 |
AOR802S - APPLIED OPERATIONS RESEARCH - 2ND OPP - JAN 2023 |
 |
1 Page 1 |
▲back to top |

nAmI BI A un IVERS ITY
OF SCIEnCE Ano TECHnOLOGY
FACULTY OF HEALTH AND APPLIED SCIENCES
DEPARTMENT OF MATHEMATICS AND STATISTICS
QUALIFICATION: Bachelor of Science in Applied Mathematics and Statistics
QUALIFICATION CODE: 08BSHM
LEVEL: 8
COURSE CODE: AOR802S
COURSE NAME: APPLIED OPERATIONSRESEARCH
SESSION: JANUARY 2023
DURATION: 3 HOURS
PAPER: THEORY
MARKS: 240 (To be Converted to 100%)
SUPPLEMENTARY/2ND OPPORTUNITY EXAMINATION QUESTION PAPER
EXAMINER
PROF.S. A. REJU
MODERATOR:
PROF.0. D. MAKINDE
INSTRUCTIONS
1. Attempt ALL the questions.
2. All written work must be done in blue or black ink and sketches must be
done in pencil.
3. Use of COMMA is not allowed as a DECIMAL POINT.
PERMISSIBLEMATERIALS
1. Non-programmable calculator without a cover.
THIS QUESTION PAPER CONSISTS OF 4 PAGES (including this front page)
Page 1 of4
 |
2 Page 2 |
▲back to top |
J
QUESTION 1 (84 MARKS]
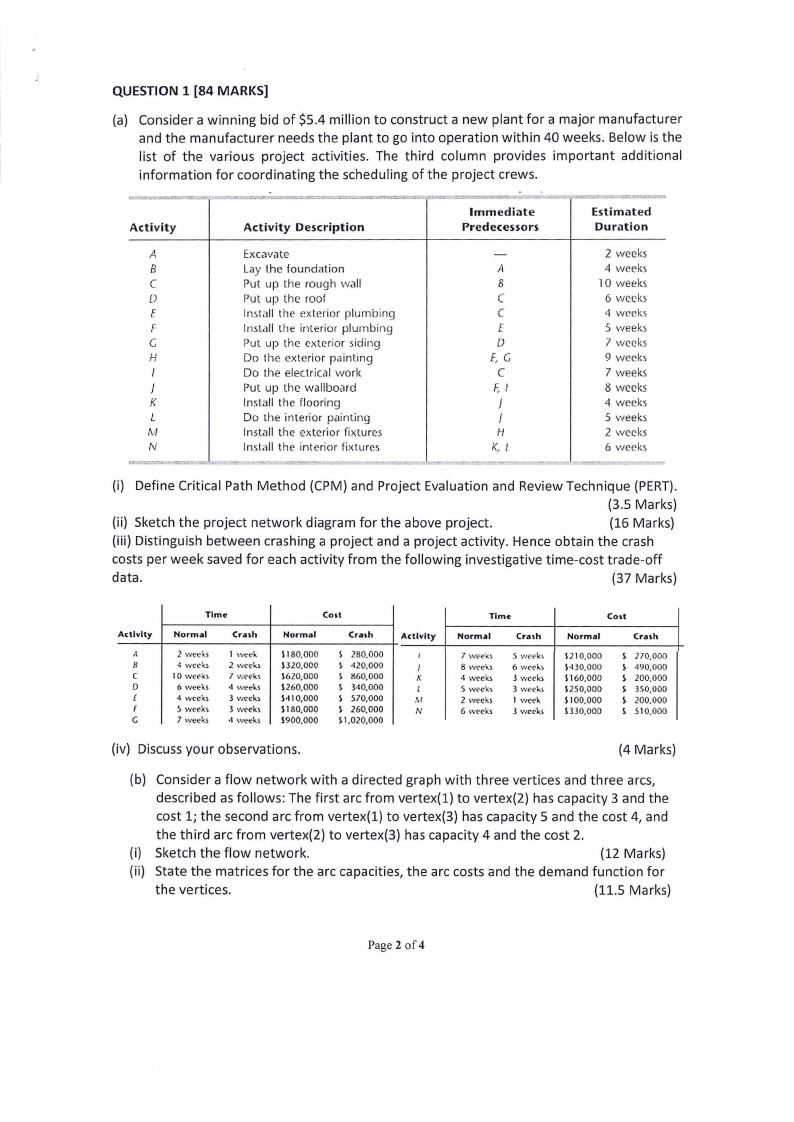
(a) Consider a winning bid of $5.4 million to construct a new plant for a major manufacturer
and the manufacturer needs the plant to go into operation within 40 weeks. Below is the
list of the various project activities. The third column provides important additional
information for coordinating the scheduling of the project crews.
"""'=
Activity
:;:w:;==::-e:,:::r-a:n::::::m:~-
Activity Description
Immediate
Predecessors
Estimated
Duration
r,..
Excavate
B
Lay the foundation
C
rut up the rough wall
D
Put up the roof
E
Install the exl·erim plumbing
F
Install the interior plumbing
G
Put up the exterior siding
H
Do lhe exterior painting
I
Do the electrical work
J
Put up the wallboard
K
Install the flooring
L
Do the interior painting
Iv/
Install the exterior fixtures
N
Install the interior fixtures
·-
2 weeks
A
4 weeks
B
10 ,,veeks
C
6 weeks
C
,1 ,,veeks
E
5 weeks
[)
7 •,veeks
E, G
9 v;eeks
C
7 ,,-.,eeks
F, I
8 weeks
I
4 weeks
I
5 ,veeks
H
2 weeks
K, I.
6 weeks
··:"#".~~
(i) Define Critical Path Method (CPM) and Project Evaluation and Review Technique (PERT).
(3.5 Marks)
(ii) Sketch the project network diagram for the above project.
(16 Marks)
(iii) Distinguish between crashing a project and a project activity. Hence obtain the crash
costs per week saved for each activity from the following investigative time-cost trade-off
data.
(37 Marks)
Activity
A
8
C
D
[
(
G
Tim"
Normal
Cra,h
2 Wt"t:ks
.; wcckl
10 werl(.s
6 weeks
4 weeks
5 weeks
7 weck.s
I Wt:l'k
2 week>
7 week,
4 weeks
3 week>
3 we~k,
4 weekJ
Coil
Norm .. 1
1180,000
1320,000
5620,000
1260,000
$410,000
I 180,000
1900,000
Cra1h
s 280,000
s •120,000
s 860,000
s 340,000
s 570,000
s 260,000
S 1,020,000
Activity
X
L
,\\•f
N
Tim"
Normal
Cra,h
7 werks
8 wl'ek.s
4 week)
5 week,
2 weekJ
6 week>
5 ',V("('k\\
6 ',\\l(•('I,._)
3 week,
3 week>
I weel,
3 wcckl
Coil
Normal
Cra,h
1210,000
1·130,000
I 160,000
5250,000
S 100,000
S330,000
270,000
,190,000
200,000
350,000
200.000
510.000
(iv) Discuss your observations.
(4 Marks)
(b) Consider a flow network with a directed graph with three vertices and three arcs,
described as follows: The first arc from vertex(l) to vertex(2) has capacity 3 and the
cost 1; the second arc from vertex(l) to vertex(3) has capacity 5 and the cost 4, and
the third arc from vertex(2) to vertex(3) has capacity 4 and the cost 2.
(i) Sketch the flow network.
(12 Marks)
(ii) State the matrices for the arc capacities, the arc costs and the demand function for
the vertices.
(11.5 Marks)
Page 2 of4
 |
3 Page 3 |
▲back to top |

QUESTION 2 [SO MARKS]
(a) Define the strategic form of a 2-Person zero-sum game, explicitly explaining its meaning.
(4 Marks)
(b) Discuss the Reduction by Dominance procedure and hence simplify by using reduction
by dominance the game defined by the following payoff matrix, showing progressively
the reduced pay-off matrix:
(18 Marks)
Player A
Player B
-51 11 AB 4 --14 2
C 3 -3 -10
D 5 -5 -4
(c) Distinguish between pure and mixed strategies.
(6 Marks)
(d) Susan has a 250-gallon capacity home heating oil tank, presently empty, meant to store
oil against the next winter. Consider the following winter heating oil quantity needed
and the oil prices during probable four levels of winter severity:
WINTER SEVERITY
Mild Winter (MW)
Average Winter (AW)
Severe Winter (SW)
Prolonged Winter (PW)
OIL STORAGENEEDED
110 Gallons
180 Gallons
230 Gallons
250 Gallons
OIL PRICESPERGALLON
N$1.00
N$1.85
N$2.00
N$3.00
Formulate a game model and employ the Minimax criterion technique to determine the
gallons of oil Susan should stockpile at the current price of N$1 per gallon to avoid oil wastage
and to maximise her saving.
(22 Marks)
QUESTION 3 [53 MARKS]
(a) Consider a competition between two companies, Coca-Cola and Pepsi, and assume the
former is thinking of cutting the price of its iconic soda. If it does so, Pepsi may have no
choice but to follow suit for its cola to retain its market share. This may result in a
significant drop in profits for both companies. Let's assume that the incremental profits
that accrue to Coca-Cola and Pepsi are as follows: If both keep prices high, profits for each
company increase by $500 million (because of normal growth in demand). If one drops
prices (i.e. defects) but the other does not (i.e. cooperates), profits increase by $750
million for the former because of greater market share and are unchanged for the latter.
If both companies reduce prices, the increase in soft drink consumption offsets the lower
price, and profits for each company increase by $250 million.
(i) Considering the above as an example of applications of Prisoner's dilemma problem,
construct the payoff matrix for each company and for the game model, taking Coca-
Cola as the row player.
(16 Marks)
(ii) What should each company do?
(7 Marks)
Page 3 of 4
 |
4 Page 4 |
▲back to top |

(b) Consider a construction firm that is deciding to specialise in building High School blocks
or Elementary School blocks or a combination of both. The construction company must
submit a bid proposal, which costs money to prepare, and there are no guarantees that
it will be awarded the contract. If the company bids on the high school, it has a 35%
chance of getting the contract, and it expects to make $162,000 net profit. However, if
the company does not get the contract, it loses $11,500. If the company bids on the
elementary school, there is a 25% chance of getting the contract, and it would net
$140,000 in profit. However, if the company does not get the contract, it will lose $5,750.
(ii) What should the construction company do?
(14 Marks)
(iii) How sensitive to the estimate of the probability of the award of a contract is the
decision (i):
• in either to build the High School or the Elementary School blocks? (6.5 Marks)
• to the net profit for each case, if awarded the contract?
(9.5 Marks)
QUESTION 4 [53 MARKS]
(a) Provide a comprehensive definition of a Decision tree and hence diagrammatically
show its basic characteristic components.
(14 Marks)
(b) Using the problem in Question 2(c) above, provide the Fold-Back method tree for its
solution.
(14 Marks)
(c)
(i) What is the Kendall's classification of Queuing Systems?
(5 Marks)
Discuss specifically the M/M/1 queuing system and the process N(t) describing its state at
time t as a birth-death process. Provide its state independent parameter equations and define
its Traffic Intensity.
(3 Marks)
(ii) Consider a drive-in banking service modelled as an M/M/1 queuing system with customer
arrival rate of 2 per minute. It is desired to have fewer than 5 customers line up 99% of the
time. How fast should the service rate be?
(6 Marks)
(iii) Trucks arrive at garage for a stop-over service according to a Poisson process at a rate of
one per every 13 minutes, and the garage service time is an exponential rate variable with
mean 9 minutes.
(iiia) Find the average number L of trucks, the average time W a truck spends in the garage,
and the average time Wq a truck spends in waiting for service.
(5 Marks)
(iiib) Due to increased traffic, suppose that the arrival rate of the trucks increases by 5%.
Find the corresponding changes in L, W, and Wq.
(5 Marks)
(iiic) Discuss your observations.
(1 Mark)
END OF EXAMINATION
TOTAL MARKS:240 CONVERTTO 100%
Page 4 of4





