 |
QCM701S - QUANTUM CHEMISTR AND SPECTROSCOPY - 1ST OPP - JUNE 2023 |
 |
1 Page 1 |
▲back to top |

n Am I BI A u n IV ERs ITY
OF SCIEnCE Ano TECHnOLOGY
FACULTYOF HEALTH, NATURAL RESOURCESAND APPLIEDSCIENCES
SCHOOL OF NATURAL AND APPLIED SCIENCES
DEPARTMENT OF BIOLOGY, CHEMISTRY AND PHYSICS
QUALIFICATION: BACHELOROF SCIENCE
QUALIFICATION CODE: 07BOSC
COURSE NAME: QUANTUM CHEMISTRYAND
MOLECULAR SPECTROSCOPY
SESSION: JUNE 2023
DURATION: 3 HOURS
LEVEL: 7
COURSE CODE: QCM701S
PAPER: THEORY
MARKS: 100
FIRSTOPPORTUNITY EXAMINATION QUESTION PAPER
EXAMINER(S) Prof Habauka M Kwaambwa
MODERATOR: Prof Edet F Archibong
INSTRUCTIONS
1. Answer ALL the SIX questions
2. Write clearly and neatly
3. Number the answers clearly
4. All written work must be done in blue or black ink
5. No books, notes and other additional aids are allowed
6. Mark all answers clearly with their respective question numbers
PERMISSIBLEMATERIALS
Non-programmable Calculators
ATTACHMENT
List of Useful Constants
THIS QUESTION PAPER CONSISTS OF 7 PAGES (Including this front page and List of Useful
Constants)
 |
2 Page 2 |
▲back to top |

QUESTION 1
[23]
(a) Define the term blackbody radiation.
(2)
(b) Explain how classical mechanics failed to explain the phenomenon of blackbody radiation
and how this phenomenon contributed to the development of quantum mechanics. (3)
(c) The Rayleigh-Jeans law of a blackbody radiation as function of wavelength is given as:
Deduce the corresponding expression and SI units of the energy density, U(v), as function
of frequency, v.
(3)
(d) Under what condition does the Rayleigh-Jeanslaw of a blackbody radiation as function of
frequency agree with blackbody radiation experimental results.
(1)
(e) Sodium metal with a work function of 2.28 eV gives off photoelectrons when it is
bombarded with ultraviolet radiation of 200 nm.
(i) Calculate the maximum possible kinetic energy and velocity of photoelectrons
emitted from Na exposed to 200 nm of light.
(6)
(ii) Calculate the wavelength required to cause photoelectron emission from Na.
(3)
(f) The derivation by Bohr of the hydrogen atom given below.
v- =Rg( -n111 - -n112) , where Rg= 109677 .58 cm·1
Calculate the wavelength, 11,(innm) and ionisation energy (in eV) for the Lyman line of the
H emission. (The n1 = 2 for the Balmer series).
(5)
2
 |
3 Page 3 |
▲back to top |

QUESTION 2
[21]
The free-electron molecular orbital (FEMO) method, which assumes that the J( electrons are
trapped in a 1-D box of length assumed to be 9.8 Aand if the Amaxwas measured to be 352
nm, answer the following questions:
(a) Calculate the zero-point energy (in eV) of the system.
(3)
(b) Why is the zero-point energy equal to zero not feasible?
(2)
(c) Determine the transition for the wavelength (Amax=352 nm) measured.
(6)
(d) Determine the number of 1t electrons and identify the HOMO and LUMO.
{3)
(e) What is the main source of error of the model in predicating the maximum wavelength
of absorption of conjugated diene molecules?
(2)
(f) For 3-dimension cubic particle-in-a-box of length 9.8 A,calculate the ground state energy
(in eV)?
(3)
(g) From the above information and calculations, the most likely conjugated diene(s) to fit
the model is/are:
(2)
(i) CH2= CH - CH = CH - CH = CH2
(ii) (CH3)2W= CH - CH = CH - CH = CH - N{CH3)2
(iii) CH2= CH - CH = CH - CH = CH - CH = CH2
3
 |
4 Page 4 |
▲back to top |
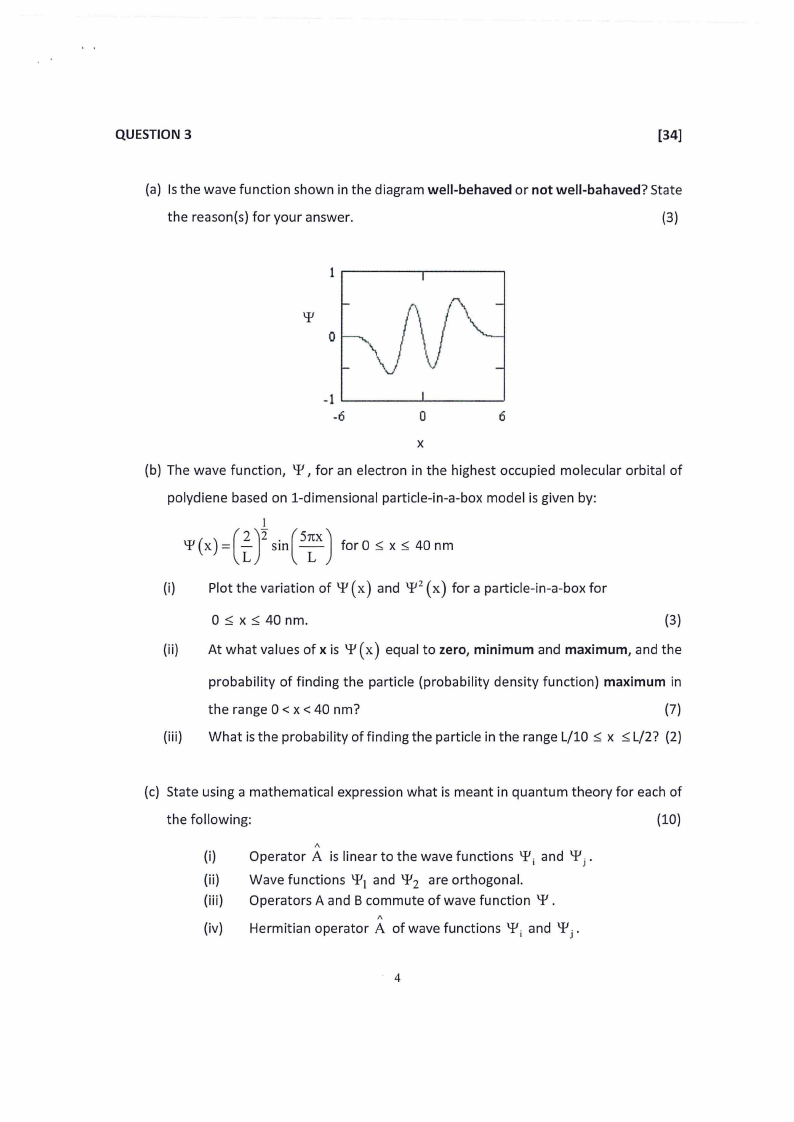
QUESTION 3
[34]
(a) Is the wave function shown in the diagram well-behaved or not well-bahaved? State
the reason(s) for your answer.
(3)
'I'
/\\
0
J
-1 ~---~----~
-6
0
6
X
(b) The wave function, 'I', for an electron in the highest occupied molecular orbital of
polydiene based on 1-dimensional particle-in-a-box model is given by:
y (5ZX) I
'I' (X)=( sin
for 0 X 40 nm
(i)
Plot the variation of 'I' ( x) and 'P2 ( x) for a particle-in-a-box for
0 x 40 nm.
(3)
(ii) At what values of xis 'I' ( x) equal to zero, minimum and maximum, and the
probability of finding the particle (probability density function) maximum in
the range O < x < 40 nm?
(7)
(iii) What is the probability of finding the particle in the range L/10 x L/2? (2)
(c) State using a mathematical expression what is meant in quantum theory for each of
the following:
(10)
/\\
(i)
Operator A is linear to the wave functions 'I'; and 'Pj.
(ii) Wave functions 'P 1 and 'P2 are orthogonal.
(iii) Operators A and B commute of wave function 'I'.
/\\
(iv) Hermitian operator A of wave functions 'I'; and 'Pi.
4
 |
5 Page 5 |
▲back to top |

(v) Expectation value,(a), of the observable A derived from a normalised
wave function ':I' .
(d) What are the physical meanings of commuting operators and orthogonal wave
functions in Quantum mechanics?
(3)
(e) Give the Schrodinger equation for a plane rigid rotor (circular motion in a fixed plane)
and show that ':I' =
ei1111
~
is an acceptable solution
of the of the operator form
of
-v2n
the plane rigid rotor Schrodinger equation. What is the eigenvalue expression? (6)
QUESTION 5
[22]
(a) Which of the species would possess
(2)
(i) Rotational microwave spectrum?
(ii) Vibrational (infrared) spectrum?
(b) Define the term selection rule using the following as examples:
(6)
(i) Particle-in-box (ii) Plane rigid rotor (iii) Simple harmonic oscillator
(iv) Anharmonic oscillator (v) Rigid rotor - Harmonic Oscillator
(c) If the degeneracy in pure rotational energy states is 7, what is the value of the
quantum number J and the possible values of the quantum number m1?
(2)
(d) The ro-vibrational spectrum is divided into three branches, namely, P, Q and R. What
is the approximate separation in terms B between the innermost line of the P and
second innermost line of the R branch?
(1)
5
 |
6 Page 6 |
▲back to top |

(e) From the ro-vibrational spectrum of 1H1271, the spacing between the peaks was
approximated to be 13.1 cm-1. Answer the following questions:
(i)
Deduce the moment inertia, I, of 1H127I.
(3)
(ii) Calculate the reduced mass of 1H127I.
(2)
(iii) Evaluate the internuclear distance (in A) of 1H127I.
(2)
Atomic masses (amu):
1H = 1.0079
1271= 126.90447
(f) The force constant of 79Br79Br is 240 Nm-1. Calculate the fundamental vibrational
wavenumber of Br2. Given: RAM for Br= 78.92 amu
(4)
END OF EXAM QUESTIONS
6
 |
7 Page 7 |
▲back to top |

LISTOF USEFULCONSTANTS:
Universal Gas constant
Boltzmann's constant,
Planck's constant
Debye-Huckel's constant,
Faraday's constant
Mass of electron
Velocity of light
Avogadro's constant
1 electron volt (eV)
R
=
k
=
h
=
A
=
F
=
me =
C
=
NA =
=
8.314 J K·1 mo1·1
1.381 X 10-23 J K·l
6.626 X 10·34 J S
0.509 (mol dm-3)112 or mo10··5kg05
96485 C mo1·1
9.109 x 10-31 kg
2.998 x 108 m s·1
6.022 X 1023
1.602 X 10"19 J
7





