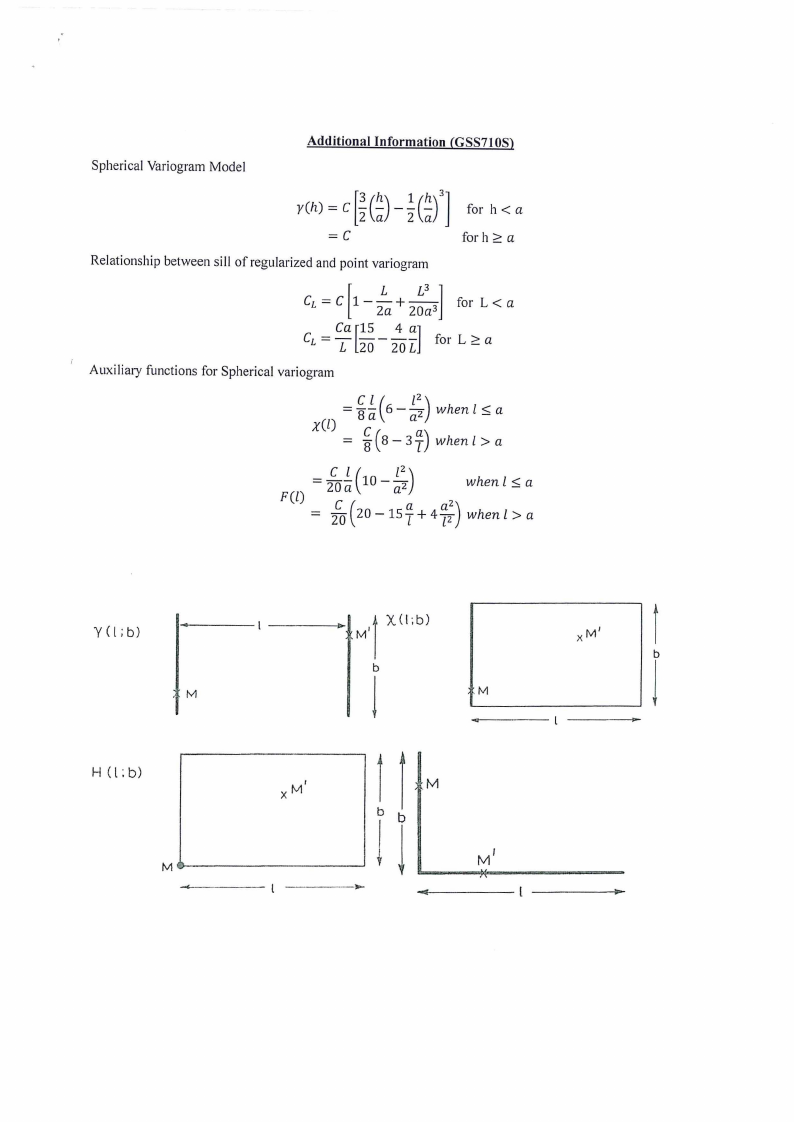
Auxiliary functionH(L,B) for Sphericalmodel with range 1.0 and sill 1.0
n
L .1 .2 .3 .4 .5 .6 .7 .8 .9 .10
.10 .114 .li7 .243 .310 .374 .436 .494 .5-16 .5!J:3 .633
.20 .177 .227 .285 .346 .406 .46-1 .518 .568 .61:3 .651
.30 .243 .28G .336 .3!)0 .-145 .4!J!) .f>50 .rm .63!) .674
.40 .310 .346 .3!)0 .439 .489 .5:l!J .586 .62!) .668 .701
.50 .:374 .40(i .H5 .48!) .5:Vi .580 .623 .663 .698 .728
.GO .-136 .464 .499 .539 .580 .621 .660 .6!)7 .728 .7G5
.70 .404 .518 .5fi0 .586 .623 .660 .696 .72~) .7fi7 .781
.80 .546 .568 .597 .629 .663 .6!J7 .72!) .758 .783 .805
.90 .593 .613 .639 .668 .698 .728 .757 .783 .806 .826
1.00 .633 .651 .674 .701 .728 .755 .781 .805 .826 .843
1.20 .6!)4 .70!) .729 .751 .774 .7!JG .818 .837 .855 .86!)
1.-10 .738 .751 .767 .786 .806 .825 .844 .8Gl .875 .888
1.60 .771 .782 .797 .81:l .830 .847 .86:l .8i8 .891 .902
1.80 .796 .806 .819 .8:34 .849 .864 .879 .892 .903 .[)13
2.00 .817 .826 .837 .850 .86-1 .878 .891 .!102 .913 .921
2.50 .853 .860 .870 .880 .891 .902 .!113 .922 .!130 .937
3.00 .878 .884 .891 .!JOO .909 .918 .!)27 .93G .!J-12 .948
3.50 .8!J5 .!JOO .907 .91-1 .922 .930 .!138 .944 .950 .95-5
4.00 .!JOS .!Jl3 .!)19 .925 .932 .!J3!) .!J-15 .051 .956 .961
5.00 .927 .!J30 .935 .040 .946 .!)51 .95Cl .961 .965 .!JG!)
fl
L 1.2 1.4 l.G 1.8 2.0 2.5 3.0 3.5 4.0 5.0
.10 .Cl!J4 .738 .771 .7!)6 .8li .Sf,:l .878 .8!)5 .908 .927
.20 .70!) .751 .782 .806 .826 .860 .88.J .900 .!113 .!J30
.30 .72!) .767 .797 .81!) .837 .870 .891 .!J07 .91!) .935
.40 .751 .786 .813 .834 .8511 .880 .900 .914 .925 .940
.50 .774 .806 .830 .849 .864 .8!11 .909 .922 .!132 .946
.60 .796 .825 .847 .864 .878 .!102 .!)JS .!)30 .9:19 .951
.70 .818 .844 .8G3 .879 .891 .913 .927 .!)38 .!J45 .%6
.80 .837 .861 .878 .8!J2 .902 .!122 .!135 .9-14 .051 .961
.!JO .855 .875 .891 .!)03 .013 .!J:lO .!)42 .950 .956 .!)65
1.00 .86!) .888 .!)02 .!Jl3 .921 .937 .948 .!)55 .!JGl .969
1.20 .8!)1 .907 .918 .927 .935 .948 .956 .96:l .067 .974
1.40 .007 .020 .030
I.GO .018 .D:JO .03!)
I.SO .027 .938 .945
2.00 .035 .944 .051
2.50 .948 .!J55 .961
3.00 .D5G .963 .067
.!)38
.!J45
.%2
.!J56
.965
.!J71
.%.I .055 .063
.051 .DG! .967
.056 .!JG5 .!)71
.DGl .96!) .!l74
.960 .075 .979
.074 .9i9 .083
.968 .072
.972 .075
.975 .078
.!)78 .080
.!)82 .084
.08::i .087
.078
.080
.983
.DS.J
.987
.!J!JO
3.50 .96:l .068 .072 .!J75 .078 .082 .085 .087 .!JS9 .!J!Jl
4.00 .!167 .072 .!175 .078 .080 .98.J .087 .98!) .D!JO .902
5.00 .974 .978 .980 .!)83 .984 .987 .990 .991 .9!J2 .094
Auxiliary function F(L; L; B) for Sphericalmodel with range 1.0 and sill 1.0
n
L .l .2 .:l ..:J .5 .G .7 .8 .9 1.0
.10 .099 .136 .178 .222 .266 .30!) .350 .390 .428 .464
.20 .168 .196 .231 .269 .:308 .347 .:l85 .423 .458 .491
.:m .23D .262 .291 .:l24 .358 .3!J4 .420 .4(i;3 .4!JG .527
.40 .311 .32!) .35:l .382 .41;3 .4.J5 .476 .508 .538 .566
.5D .380 .395 ..JIG .441 .-.168 .-.197 .526 .554 .581 .607
.GD .-145 .45!J .477 .49!) .523 .549 .574 .GOO .624 .G4S
.70 .507 .51!) .535 .554 .576 .508 .622 .6-1.J .GG6 .687
.so .565 .574 .58S .606 .G2f, .6-15 .GG6 .686 .705 .724
.90 .GIG .625 .637 .652 .GGD .687 .706 .724 .741 .757
1.00 .662 .660 .680 .694 .709 .725 .741 .757 .772 .786
1.20 .735 .741 .750 .760 .772 .78-5 .rn7 .810 .822 .833
1.40 .i89 .7!J4 .800 .809 .818 .82S .83!) .840 .858 .867
1.60 .828 .832 .838 .845 .852 .861 .86!) .877 .885 .892
1.80 .858 .861 .866 .872 .878 .88f> .802 .8!J9 .!)05 .Dll
2.DO .880 .883 .887 .802 .8!)7 .003 .009 .915 .920 .025
2.50 .918 .020 .!)23 .926 .930 .934 .938 .942 .9-16 .049
3.00 .!l40 .041 .D-14 .!J4G .940 .!)52 .%5 .958 .!160 .DG3
3.50 .954 .955 .957 .950 .!JG! .06:l .!JGG .068 .970 .972
4.00 .!)63 .964 .065 .967 .!JGD .070 .072 .074 .976 .977
5.00 .974 .075 .976 .!J78 .97!) .080 .!J81 .983 .!JS-I .985
L
.10
.20
.30
.40
.50
.GO
.70
.80
.DO
1.00
1.20
1.40
I.GO
1.80
2.00
2.50
3.00
:1.50
4.00
5.00
B
1.2 1.4 l.G 1.8 2.0 '_J_ ;•J 3.0 3.5 4.0 5.0
.526 .:j77 .Gl!J .653 .683 .738 .777 .807 .820 .861
.550 .508 .638 .671 .699 .751 .78!) .SlG .837 .868
.581 .626 .663 .603 .710 .768 .80:l .820 .84!) .877
.GIG .6G7 .GDl .71!) .742 .787 .Sl!J .843 .861 .887
.652 .GSD .720 .745 .767 .808 .836 .858 .874 .808
.688 .722 .740 .772 .791 828 .854 .873 .887 .900
.723 .753 .777 .798 .815 .847 .870 .887 .900 .919
.756 .782 .804 .822 .837 .865 .886 .901 .012 .029
.785 .SOD .828 .84:3 .857 .882 .900 .013 .923 .937
.811 .832 .8.JD .862 .874 .806 .!Jl2 .023 .9:32 .045
.853 .869 .882 .803 .902 .Dl!J .031 .040 .947 .057
.883 .896 .DOG .9F, .022 .036 .945 .952 .958 .966
.!J05 .915 .924 .!)31 .037 .048 .OGG .%1 .!JGG .072
.022 .030 .037 .04:3 .048 .057 .96:3 .068 .972 .077
.!J3.J .041 .047 .052 .956 .064 .!JG!J .073 .976 .981
.955 .DGO .064 .DG7 .970 .075 .!)79 .082 .084 .987
.067 .071 .!J74 .076 .078 .082 .085 .!J87 .088 .DDl
.97:"i .078 .080 .982 .DS'.l .986 .088 .D!JO .DDl .!JD3
.080 .982 .084 .DSG .087 .089 .DDl .092 .003 .904
.087 .088 .98!) .9!)0 .DDl .!JD3 .DD'1 .095 .005 .906