 |
MPC711S - Mineral Separation Processing - 1st Opp - June 2022 |
 |
1 Page 1 |
▲back to top |

n Am I BI A u n IVER s ITY
OFSCIEnCEAno TECHnOLOGY
FACULTY OF ENGINEERING
DEPARTMENT OF MINING AND PROCESS ENGINEERING
QUALIFICATION : BACHELOR OF ENGINEERING IN METALLURGY, CHEMICAL
ENGINEERING & MINING ENGINEERING
QUALIFICATION CODE: BSc.
COURSE CODE: MIP710S; MPC711S
LEVEL: 7
COURSE NAME: MINERAL PROCESSING 314 &
MINERAL SEPARATION PROCESSES
SESSION: APRIL 2022
DURATION: 3 HOURS
PAPER: THEORY
MARKS:60
EXAMINER(S)
MODERATOR:
FIRST OPPORTUNITY QUESTION PAPER
Dr. Clement K. Owusu
Mr. Thomas Moongo
Prof. Godfrey Dzinomwa
INSTRUCTIONS
1. Answer all questions.
2. Read all the questions carefully before answering.
3. Marks for each questions are indicated at the end of each question.
4. Please ensure that your writing is legible, neat and presentable.
PERMISSIBLE MATERIALS
1. Examination paper.
THIS QUESTION PAPER CONSISTS OF 3 PAGES (Including this front page)
1
 |
2 Page 2 |
▲back to top |

Question 1
a) Representative sample of galena ore is required for metallurgical testing at
laboratory. The assay for the galena ore is 15% at a confidence level of ±0.1%
Pb at 2o standard deviation. The galena is liberated at a size of 75 µm. Assuming
the top size of the ore from the sampler is 1.5 cm and the estimated lower size
is 0.2 cm. Estimate the minimum mass required for the test work. The density
of galena and quartz as 7.6 g/ cm3 and 2.65 cm3 respectively. (Assume shapefactor
(fJof 0.5 except for gold ores where the factor is 0.2; for size distribution factor (g), if
d95/d5>4, g=0.25; d95/d5 is between 2 and 4, g = 0.5; d95/d5<2, g=0.75; d95/d5=1,
g=l; molar mass of Pb and Sare 207.2 g/mol and 32.07 g/mol respectively) (8 marks)
b) An ore deposit after mineralogical analysis was found to contain minerals A
and B. The specific gravity of minerals A and B respectively are 3.3 g/ cm 3 and
1.9 g/ cm 3. A company consulted you and wish to know whether or not mineral
A (mineral of interest) could be separated from mineral B (gangue) using
gravity concentrator. What will be your recommendation and why? (Take the
specific gravity of the fluid medium as 1.3 g/ cm3)
(2 marks)
c) Despite improvement on safe design for tailing dams, there has been reported
failure almost every year for the past 30 years. Discuss 3 possible causes for the
failures of the tailings dam.
(6 marks)
Question 2
a) A flotation plant has been optimised to selectively float lead and zinc from an
ore comprising of galena (PbS), sphalerite (ZnS), chalcopyrite (CuFeS2) and
pyrite (FeS2).After froth flotation, the concentrate was found to contain Zn, Pb,
Cu and Fe content of 48.6%, 57.6% 1.6% and 26.5% respectively. Estimate the
percentage of galena, sphalerite, chalcopyrite and pyrite in the concentrate.
(Molar mass of Zn, Pb, Cu, Fe and Sare 65.38 g/mol, 207.2 g/mol, 63.55 g/mol,
55.85 g/mol and 32.07 g/mol respectively)
(8 1narks)
b) A single cell in a given bank of flotation cell gives copper recovery of 45% for a
residence time of 5 minutes. What is the number of similar sized cells in a
continuous flotation bank required to achieve a total recovery of 95%?
(5 marks)
2
 |
3 Page 3 |
▲back to top |
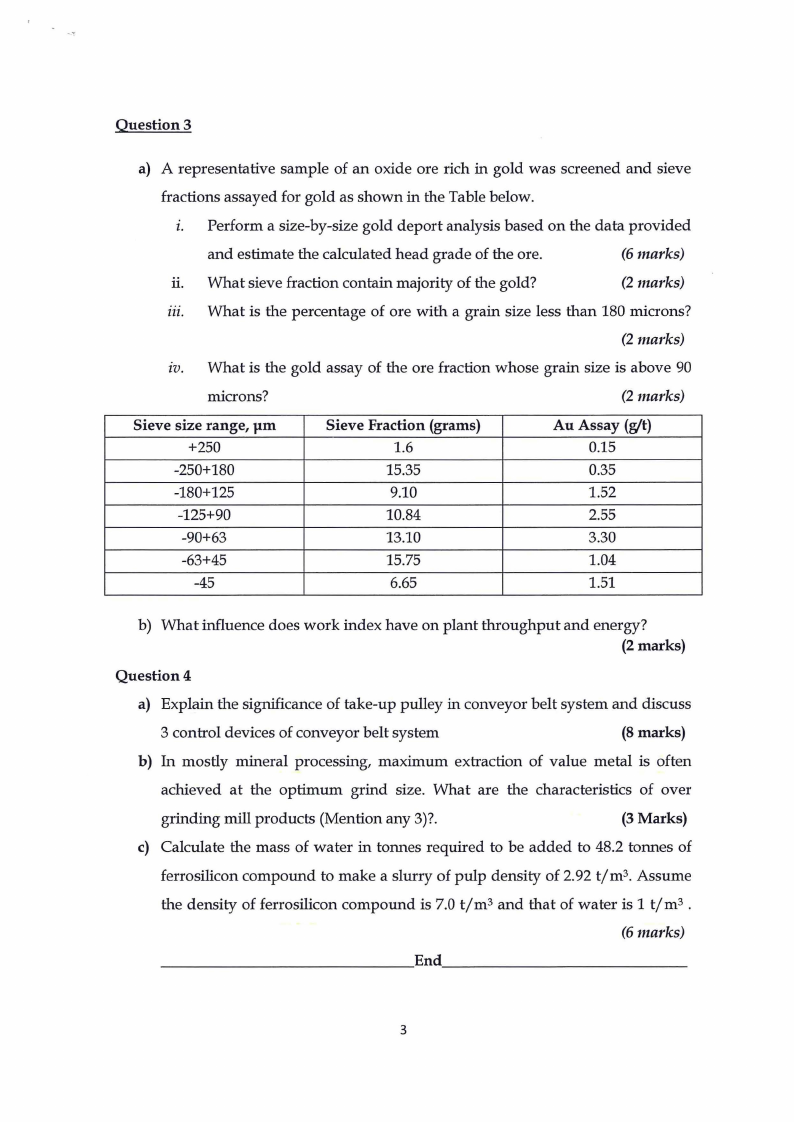
Question 3
a) A representative sample of an oxide ore rich in gold was screened and sieve
fractions assayed for gold as shown in the Table below.
z. Perform a size-by-size gold deport analysis based on the data provided
and estimate the calculated head grade of the ore.
(6 marks)
ii. What sieve fraction contain majority of the gold?
(2 marks)
m. What is the percentage of ore with a grain size less than 180 microns?
(2 marks)
zv. What is the gold assay of the ore fraction whose grain size is above 90
microns?
(2 marks)
Sieve size range, µm
+250
-250+180
-180+125
-125+90
-90+63
-63+45
-45
Sieve Fraction (grams)
1.6
15.35
9.10
10.84
13.10
15.75
6.65
Au Assay (git)
0.15
0.35
1.52
2.55
3.30
1.04
1.51
b) What influence does work index have on plant throughput and energy?
(2 marks)
Question4
a) Explain the significance of take-up pulley in conveyor belt system and discuss
3 control devices of conveyor belt system
(8 marks)
b) In mostly mineral processing, maximum extraction of value metal is often
achieved at the optimum grind size. What are the characteristics of over
grinding mill products (Mention any 3)?.
(3 Marks)
c) Calculate the mass of water in tonnes required to be added to 48.2 tonnes of
ferrosilicon compound to make a slurry of pulp density of 2.92 t/m 3• Assume
the density of ferrosilicon compound is 7.0 t/m 3 and that of water is 1 t/m 3 .
(6 marks)
--------------
End·--------------
3
 |
4 Page 4 |
▲back to top |






