 |
NUM702S - NUMERICAL METHODS 2 - 2ND OPP - JANAURY 2025 |
 |
1 Page 1 |
▲back to top |

n Am I BI A uni VER s I TY
OF SCIEnCE TECHnOLOGY
FacultyofHealthN, atural
ResourceasndApplied
Sciences
Schoolof NaturalandApplied
Sciences
Departmentof Mathematics,
StatisticsandActuarialScience
13JacksonKaujeuaStreet
PrivateBag13388
Windhoek
NAMIBIA
T: +264612072913
E: msas@nust.na
W: www.nust.na
QUALIFICATION: BACHELOR OF SCIENCE IN APPLIED MATHEMATICS AND STATISTICS
QUALIFICATION CODE: 07BSAM
LEVEL:7
COURSE:NUMERICAL METHODS 2
COURSECODE: NUM702S
DATE: JANUARY 2025
SESSION: 1
DURATION: 3 HOURS
MARKS: 90
SUPPLEMENTARY/SECOND OPPORTUNITY: QUESTION PAPER
EXAMINER:
MODERATOR:
Dr SN NEOSSI-NGUETCHUE
Prof S.S. MOTSA
INSTRUCTIONS:
1. Answer ALL the questions in the booklet provided.
2. Show clearly all the steps used in the calculations. All numerical results must be
given using 5 decimals where necessary unless mentioned otherwise.
3. All written work must be done in blue or black ink and sketches must be done in
pencil
PERMISSIBLE MATERIALS:
1. Non-Programmable Calculator
ATTACHEMENTS
None
This paper consists of 3 pages including this front page
 |
2 Page 2 |
▲back to top |

Problem 1 [25 Marks]
1- 1. Esta bl'1sh t he p ad,e approxn.nat10. n
ex ::::R:;3,3(x ) =
120
120
+_
6600xx
++
1122xx22 +_
xx
3
3
[13]
1-2-1. Find the Fourier sine series for the 27T-periodicfunction f(x) = x(7T- x) on (0, 7r).
[9]
1-2-2. Use its Fourier representation to find the value of the infinite series.
[3]
Problem 2 [20 Marks]
1--+-3-13-+-+5·13
1
73
1
93
..
For any non negative interger n the Chebyshev polynomial of the first kind of degree n is defined as
Tn(x) = cos [ncos- 1(x)], for x E [-1, l].
2-1. Show the following property
[10]
f < Tm, Tn>-_
0, m=/n,
1
-1
-T-m-J-(lx)-Tnx(2x)
d_
X-
{
7T,
7T
2'
m = n = 0,
m = n # 0.
2-2. The property in 2-1. allows us to define the Chebyshev series of f(x) as follows
L f (x) ~
00
1
'ckTk(x) = 2caTo(x) + c1T1(x) + c2T2(x) + · · ·
k=O
where ck =< f, Tk > / < Tk, Tk > for k 1 and co/2 =< f, To > /7T
2-2-1. Determine the Chebyshev series expansion of f(x) = Jl - x2.
[10]
Problem 3 [19 Marks]
3-1. Given the integral
[1 ~dx = 1.6
10.04 V X
3-1-1. Compute T(J) = R(J, 0) for J = 0, 1, 2, 3, 4 using the recursive Trapezoidal rule.
[15]
3-1-2. State the two-point and the three-point Gaussian quadrature rules respectively for a continuous
function f over the interval [-1, 1].
[4]
Problem 4 [26 Marks]
4-1. Assume a 3 x 3 matrix A is known to have three different real eigenvalues -\\1, -\\2 and -\\3. Assume we
know that -\\1 is near -2, -\\2 is near -5 and -\\3 is near -1.
4-1-1. Explain how the power method can be used to find the values of -\\1, /\\2 and -\\3 respectively. [2x3=6]
4-1-2. Discuss how shifting can be used in 4-1-1. to accelerate the convergence of the power method. [2]
1
 |
3 Page 3 |
▲back to top |
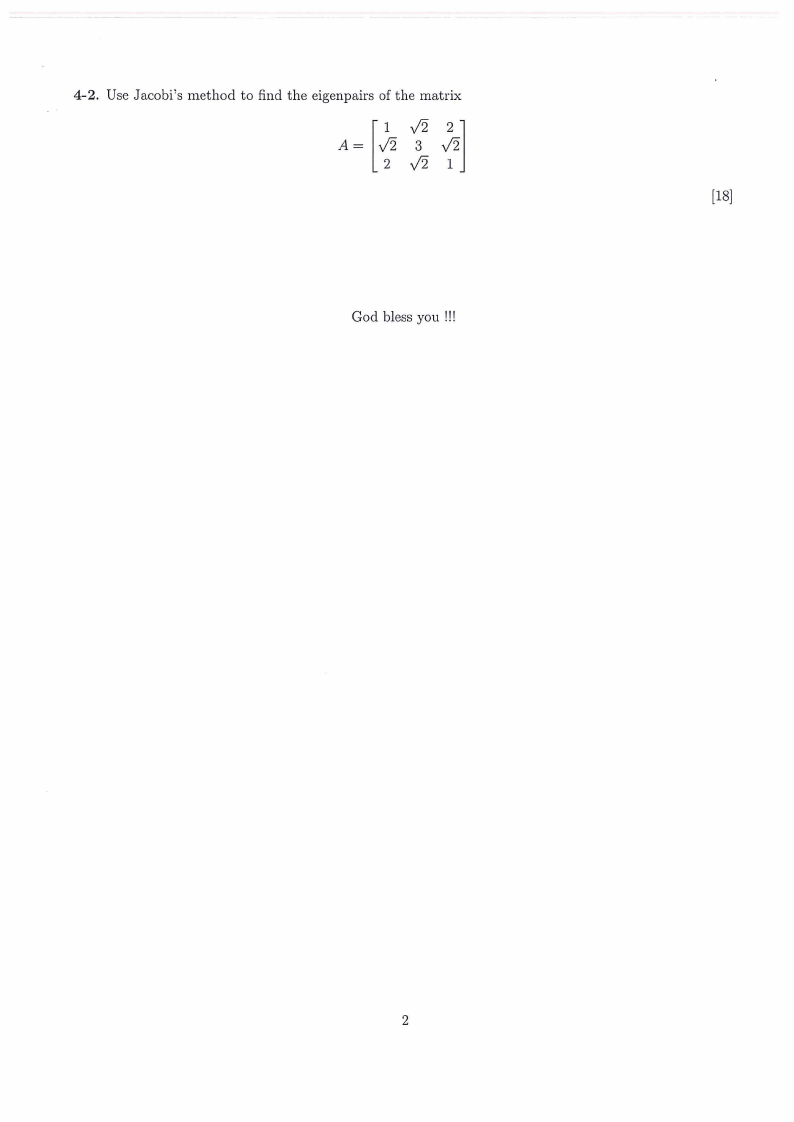
4-2. Use Jacobi's method to find the eigenpairs of the matrix
l 2] A=
J2
J2
3
J2
[2 J2 1
[18]
God bless you !!!
2





