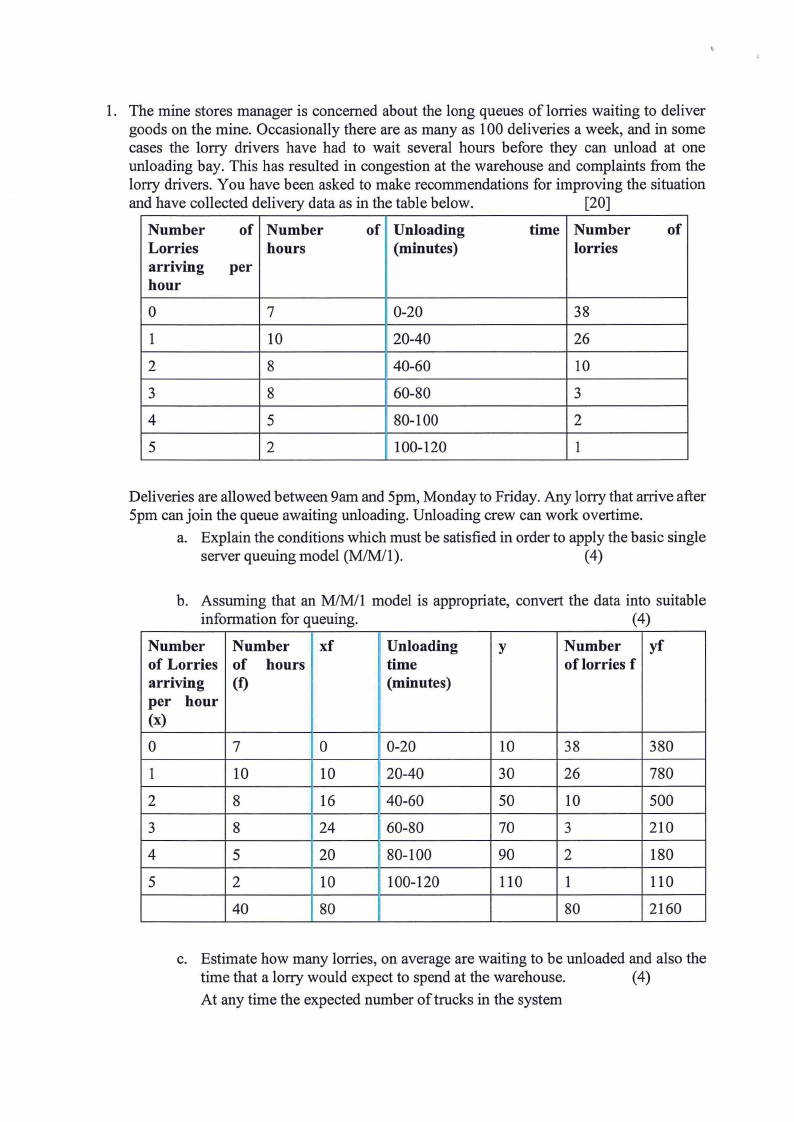
TABLE1
S1Jndardnorn1JIcurve areas
~,d~ca
'.
0
•POZ <:I
=
11.00 0.01
II.Ill
0.113 o.o.a 0.05
0.06
0.07
0.08
0.09
0.0 0.5000 0.50-lO 0.5080 0.5120 0.5160 0.5199 0.5231) 0.5279 0.53l'J 0.5359
0.1 0.5''JS 0.5-1'S 0.5-178 0.5517 0.5557 0.55')6 0.56 6 0.5675 0.571-1 0.5753
0.2 0.571JJ 0.5832 0.5S7I 0.591()
o.59S7 0.6026 0.(l{X).l 0.6103 0.61-11
0.3 0.6li9 0.6217 0.6255 0.6293 0.6331 ll.636S 0.6-106
0.6-ISO 0.6517
0.-l 0.655-1 0.6591 0.662 0.666-1 ll.6m) 0.6736 0.6772 0.6SO'
0.6879
0.5 0.6915 0.61J50 0.6'JS5 0.7011) 0.705-1 0.7USS 0.712' 0.7157 0.71')(} 0.722-1
0.6 0.7_57 0.7291 0.732-1 0.7357 0.73,'9 0.7-122 0.7-15-1 0.7-1.'6 0.7517 0.75-19
ll.7 0.75Sll 0.7611 0.76-12 ll.7673 0.77()-1 0.7Hl 0.776-1 0.779-1 0.7S2J 0.7852
0.S 0.7SSI 0.7910 0.71J31J 0.7%7 0.791)5 O.St.m ll.8051 0.S07S 0., 106 0. 133
0.9 U.8159 0.8186 0.8212 0.S23S 0 826-1 0.8289 0., '15 U.83-10 O.S365 O.S'S1J
1.0 O.S-I1J O.S-13S U.8-161 o..--lS5
I. I ll.S6-IJ U.S665 O.S6'6 0.S70S
1.2 0.8.'-19 O.S.'61J o.ssss 0.81)()7
I.
(1.1)032 O.'XJ-19 ()_<J()(\\6 0.90S2
1.-1 0.9192 0.9207 o.1J_22 0.92'6
O.S50S
1Ul729
O.S1J25
o.•JO<)'J
O.'J25I
0.8531
0.S7-11J
0.9115
0.9265
0.855-1
0.8770
0. 962
0.91 'I
0.9279
0. '577
O.S 90
O.S').'0
0.1Jl47
0.1J29_
0.8599
o.s·JO
0 .• 997
U.9162
0.9'06
0.86_)
0..'SJO
0.9015
0.9177
U.9319
1.5 O.<J32 U1.J -15 0.9357 0.9370 0.93S2 0.9'9-1 0.9-106 0.9-11, 0.'J-1_1) 0.9-141
1.6 0.1)-152 0.9-16 0.9-17-1 0.9-IS-I 0.9-11)5 0.9 05 0.1J 15 U.9525 ll.lJ'35 0.9545
1.7 0.955-1 0.')5(H ll.957' 0.9582 0.1)591 0.95')<) U.96US 0.<J616 0.'J625 0.963'
I.S ll.1J6-II ll.'./6-19 O.'J656 U.966-1 0.%71 o.%78 0.%,'6 0.'J6•)' 0.9699 0.9706
1.9 O.'J713 0.1J71'J 0.1J726 0.9732 0.'JTS U.97+1 0.9750 lU756 0.9761 (J.1)767
2.U U.9772 ll.977S o.cmu U.'J7SS 0.'J7'J' 0.971).' 0.'JS03 O.'J·o · U.9'12 0.9817
2.1 0.9.'21 U.9S26 0.%30 0.983-1 0.'JS'8
U.9S-16 O.'JS5ll 0.9.'5-I 0.9S57
2.2 0.'JS61 O.'JS6-I 0.9S6li 11.9871 0.'Jli75 U.9S7S 0.'JSSI U.9.'S-1 U.9'li7 0.9S')(J
2.3 0.9S93 0.'J 096 0.9S9S 0.'J')(JI o.•J9<)-I 0.'Nll6 111..l<JU'J 0.9911 0.9913 0.9')16
1.-l 0.99IS 0.9920 O.'J<J22 0.')925 ll.'J927 ()_')1)_1) ll.'.l'J I 0.9932 0.993-1 ll.9'J36
2.5 ll.'J93li O.'.l'J-10 0.99-11 0.1J1J-13 0.')9-15 ll.1.l'J-16 0.'.l'J-IS 0.99-l'J 0.9951 O.'J<J5_
2.6 0.1)95 0.9')55 0.1J<J56 0.')957 0.9959 U.9'J60 0.9'J61 0.9962 U.9%3 U.9'J6-I
2.7 0.9965 0.'.1')66 0.1.1')67 0.9968 ()_•)%') 0.'J'J70 0.9'J71 11.9972 ll.')973 U.9'J -l
2.li 0.997-1 0.9'J75 O.<J<J76 0.'J1J77 11.9977 U.9'J7S O.'.l'J7'J 0.9979 0.99SO IJ.'J'JSI
2.'J 0.99SI 0.9')S2 0.9'JS2 0.99S U.')9~
0.'.l'JS5 O.'Jt),'5 0.99,'6 0.1J'J,'6
3.0 O.'J9S7 0.99S7 0.'NS7 0.91JSS 0.1J'JSS U.'.l'JS9 11.'NS9 O.'J9S1J 0.9')')() 0.9'J90
3.1 ll.91J90 0.9')91 U1.J<1JI 0.'J'.l'JI 0.'J'J'J2 O.'J'J'J2 O.'.l'J'J2 U.99'J2 0.'J99J 0.'.1')')3
32
ll.999.I 0,9')9.3 0.'.l'J'J-1 ()_(/1)').j
0.1J1J9-l 0.')1)9.J 0.'.1')9-1 0.99')
0.99<)5 ll.'.l'J'J5
3.3 U.9995
3.-1 0.')')')7
0.')')95
0.9'J97
0.9')95
ll.1.l'J97
O.'J9'J6 0.99% O.'J'J'J6 O.'J<J96 0.')')')6
0.99')7 0.9\\J<J7 {)_1)')1)7 0.')')')7
0.99'J7
0.')996
0.')1)97
U.')'JIJ7
0.')')9S