..'.'
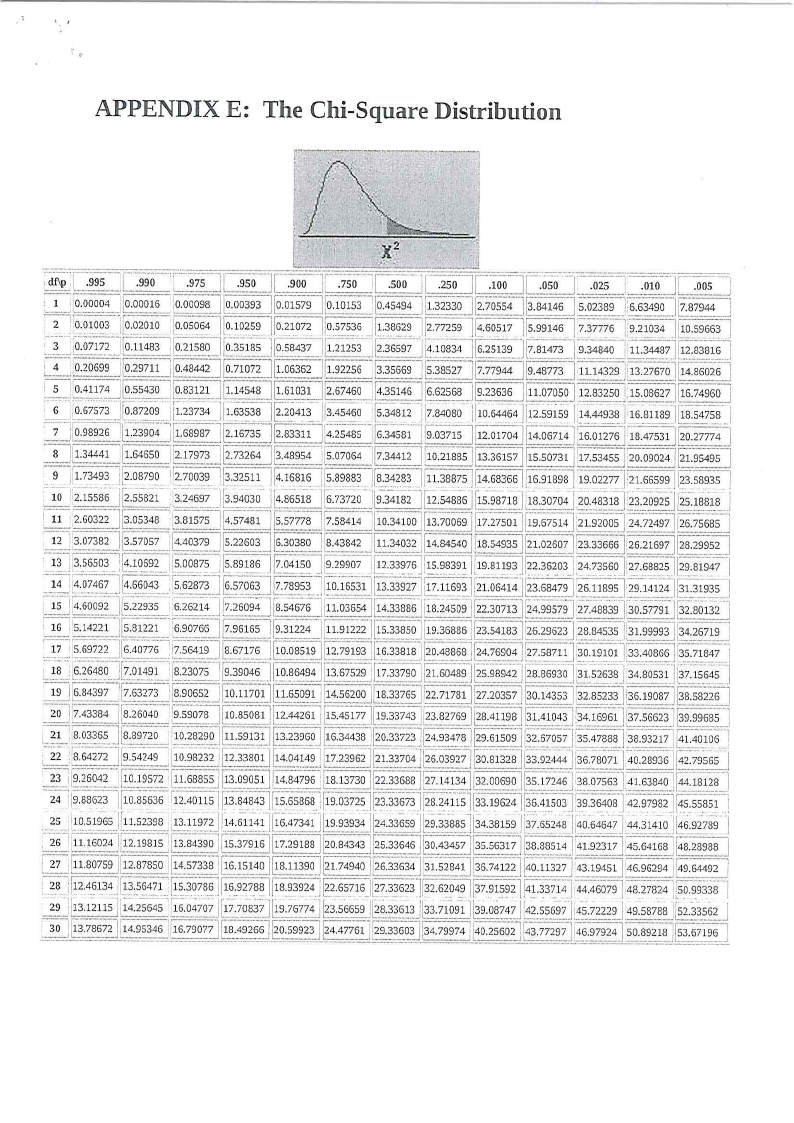
APPENDIX E: The Chi-Square Distribution
'.~...1-·.995·-.1:;1;;;···--·;-]·:I;;.9755011-·:900-r·:1-7so[·sool-l··.2501-1""":l·o1"1.o050i,-·:·o··i1s· :oio1'"1····.·o·o·1s
,1 _,_:0.000l0lo4.000i106.000J9l8o.00319130.01151709.10!1lo5.3454J9!u4233l0p.705]5143.8411456.o2319:96.634[j970.879l44
2 1'0:0~01~;39.9_2to~.10050l~[o_._1[l0o2.2~10l7fo2:_~2.~.1.~.61:3_.181~2.97-7l2l~5-960511175.99l1,74.6377]796.2_1._1.:0.913·4_5_9.~~3]
,:3...;o.07172~]10T.1o1.42813l?_~s:_~s-_1ia~o~~]_~]31!]1.212I[523.'.~~Jl~~?:._.71-o[_~~~1~-_~lJ7_-i-]~.1~-~...1-_~:3.~11~2~.°8-3]:8_116_.1:_3
:_~..0. .2069IJ9o.297:1101.484ll4o2.71017121.06131612.921235.635616195.38151277.7719[494.48717,131.14329113.2767I01114.8
i~ _:_10.4117ll4o.554[3o0.83112111.14151418.61101321.67,41640.351416.62151698.231613161.0I71025.8032l,5105.08627111i 6.74960
,~_6 i~:675J[7o3~87J2i0'.~93fj_4___ll1.~i~s]~?04"1:~3~--3ll~i·481~1~2?~.804l0l_8100. .6~~6~J1li:~.1-~-i~9.3~J:1~·!!189']li'a:s4
·_!._;[o.98791216.239i~0:4~-~9.~2__1~.16713154].22.58143§834515181]19.037J~125.01704]l14.06714118:.1467.503112J7i62]01.27774
--i]l1.3444111.64615102.171927.373216143.48·91554.07016147.34l4l1102.21B851[13.361i5l1771.1513[542.5055.007930l[12241.95[495
-~--sJ·f-t-.·734j9j2~.-08719:~i1?o3~9-71131.342.15611~1[_51.8~98ll8.8~.:~~ll218L~38j8f7154:683661JI1169..90128_92Bn.J:2"~66~9I 9-]l~3.5
,~io-1i~~~]12.ss82.~.1.246~7-J!3.i:l.49..8~6?-3J5~?1.=783- 7-2[109~341a2-][12.548861[15.987-~J~:~?~:Ji_o_.;4_8i:~~~!
~-112·.60321213.05,334.81517/54.57418115.57l7/i7s8s41·;·-·:110.341l0l0i71.121735.071010[6i-99~6-7Si4'ln./9122060.7S5rI2648~57249
·_!_~3_.0:7381213.57:01547.40317195.22151063.30131880.4318~412:~:o~~_llf141.88.4554il4920315.0_26?.?Ji23.336661!2_6I .216971
-]~]3~56-5!10~3:ios~~?.0--(i)8?5-~).8.1l9?1_8-064_1!,9~.~299i0!172.~3r~1?5.~.6?].-B3Sn7I11~129..38J~1.2~4_9.03733J5:~~0.6~8I122~~~19I 47
--~~l;io;;~}.6604_3':s.628J7136:57J0t.673895.3[lo:"i615133i°.l33'.9n2171169[~iil~41I4123.681427G9~iwsJ2ii~[134u1023;·51-I
!FG00i9[2~i~~·6~.2-6211147·~· 2--·6101984.5.I4l16°7i6:0. 3654.fflii'i4s:.323485l[802692~ii-234].99527i9:4]8839o.l-si791'1[3·12:sa1i2
;~::~15~.1~4, 2]2115.812·.2~1:??1-7?.9:61~161]5~i"i2121;~~~~~f1-5~.23~3_18:~5J0~:~~1:~2_38.564:12863.2196231281.:83415.939I513949.3267·19
~_-1?:_:i~_:1_~[6_9.-4?._o~i1i2-76:-:-s,·s1d~i:g_.6]_J._7[_i.~o?·.6:o[1_?-~2.?.:.1~[91--~_36_]_] .§3:~.418-~_.~1J~274~6.-9! oj'.4.~?. ~s!:in~~o-:19~.~i]:33.4086~
1~-_~:s·;~:ii,i~~~is~o1-~~]~:~~1~f9~..3?:9·?0~.41J6_..1.?~~l~.13.=..:~.~-.~7[Ji-i~.3~3--.i:g·a-l I~-~.:9-[82-?s~.~a~6I~9iio~Jsj~-~:i~~~Jot~_7s-i:1X-lsI.G~s.--
!16.84i3l977.63211783.906:[5i.21o. 1?0Jl1n.650:9[11::~~~9~__l1b1.71187.38li312776.25035711l3,~02.1-4~38i5-3?362.~139-087113I8.58226
~~~~J7.4313l88:4~.~.J~9:.?590718110.850811i1[12s.454l12l176971.33743[123.827691[28.411981!31.J4[13094.9391I6i38:5:1-~~
l--ii:'18.03..31.6158_.89'71200.28290][1.1.151931.32]131966.034[42308.33723/§741.92394.671813520.9617052_J'3J s,47888
: 22_:1_a:_6427[29-~]542[4ioS.:98232-:[li[iii4s.o014·1I14197:23[926i32317I-04
133.92444·11;·4306:.2738ll904:7z3i'~5"7·91555
i19.260'14~2.~.9?:.~?~.L~~_I~8[-?~?~J:?.~1°1--~~~:~.]1~1?8.~.1~3I/72320.33I69781-8::_4!~:.11I3123.50.0167:9:2.0~4~6·?.74~1~.633.8.!144:04.18j128
---24i9-·.s: a6--2i[i-a3.ss63161·2.40I[1ji1~5~~141~15:61_151~96.801_317~~:~1:336731[13~3~.1-9-1261~2~1451.·:;4;3~9s.o336J4I-o4a2.97_19[4852.55~151
·- 25..:'.~°-:~-~9~~![11.52!3~9::8~~~-l[lG.47341-·1119.939341124.33659·1129.3:3885_[4]163.94..~:3.1.?8~19591:~
,~~1s1_.1-6l0/2142.19!811153.84![31950.379161!17.291,8182151.32306.84463Jl433o.43457113_I54.15.693213/1741157[.63481.8688511144J8.28988
!.!?J11.80I7J5192.8718151o4.51[7i3.3~8TI~Jr:n~.111319201.749401113216:s.3230603J;4316.741221140.11114362.97612'4934.1194195.164492
!--2!1Ii~"'2-~1'_[~3:~_5~l4~_~?-.~10_I17:186~:92II17R_89~39:§2_42~6_5I~_77_1:36·~1/362.36~I?[347~.91I_l4~i:~3~23~;:i::446]07:;9118,2:]7'.5892,49.~.I.9338
·--~~--111l[3i4.1.2-25161455'i"i-6.0470-71r1i-[72-3.7.506l8l63257s9.J3li39J6.l173367.771·41D193i9.08747114~:~?-~?...Zli:s]21.435.3.I752622914
~~!ol1-3.78161n14.:~li51364.769o771/1!l82.04.9s29[69l.2643..477611129.33~~31134.799741r.;:l·'oso:2:as69022i~-J]Jl4~3~.;7~7;~29;~:J.J_