 |
PBT501S - PROBABILITY THEORY 1 - 2ND OPP - JANUARY 2025 |
 |
1 Page 1 |
▲back to top |

nAmlBIA UnlVERSITY
OF SCIEnCEAnDTECHnOLOGY
FacultyofHealthN, atural
ResourceasndApplied
Sciences
Schoool f NaturalandApplied
Sciences
Departmentof Mathematics,
StatisticsandActuarialScience
13JacksonKaujeuaStreet
Private Bag13388
Windhoek
NAMIBIA
T: +264612072913
E: msas@nust.na
W: www.nust.na
QUALIFICATION : Bachelor of Science in Applied Mathematics and Statistics & Bachelor
of Science
QUALIFICATION CODE: 07BSAM & 07BOS
LEVEL: 5
COURSE:PROBABILITY THEORY 1
COURSECODE: PBTS0lS
DATE: JANUARY 2025
SESSION: 1
DURATION: 3 HOURS
MARKS: 100
SECONDOPPORTUNITY/SUPPLEMENTARYE:XAMINATIONQUESTIONPAPER
EXAMINER:
MODERATOR:
Dr D Ntirampeba
Mr J Amunyela
INSTRUCTIONS:
1. Answer all questions on the separate answer sheet.
2. Please write neatly and legibly.
3. Do not use the left side margin of the exam paper. This must be allowed for the
examiner.
4. No books, notes and other additional aids are allowed.
5. Write all answers clearly with their respective question numbers.
PERMISSIBLME ATERIALS:
1. Non-Programmable Calculator
ATTACHEMENTS
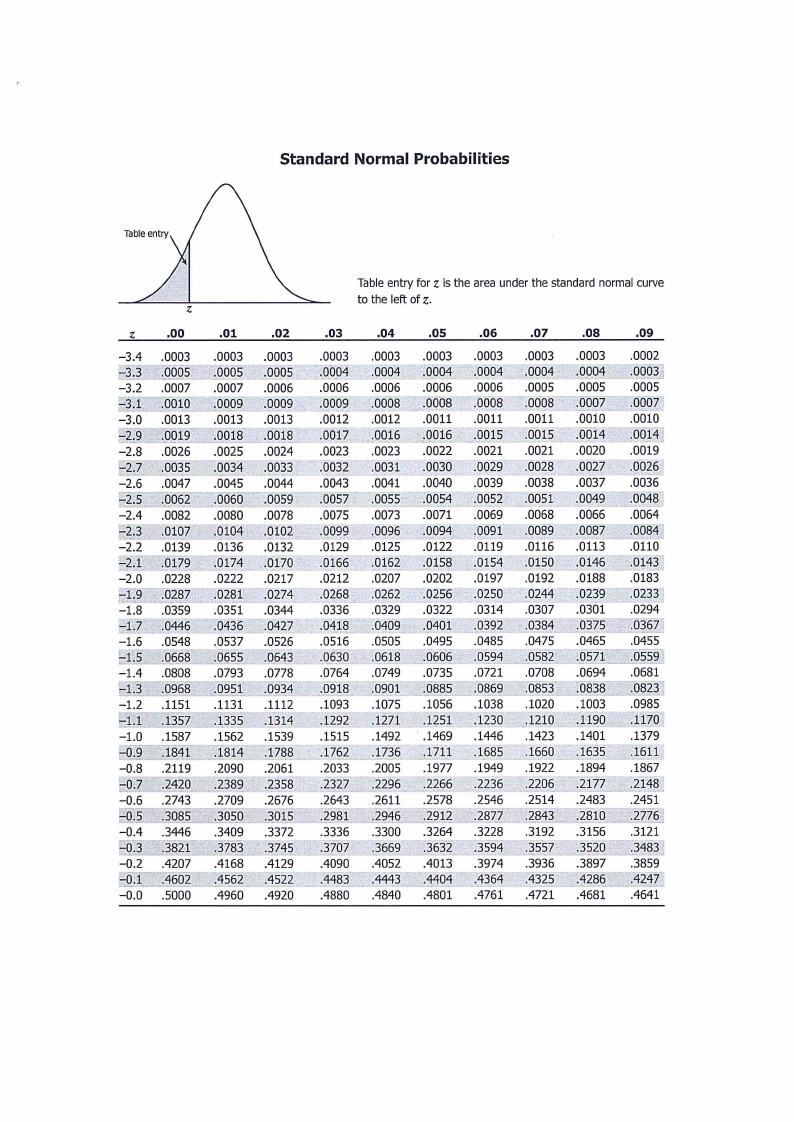
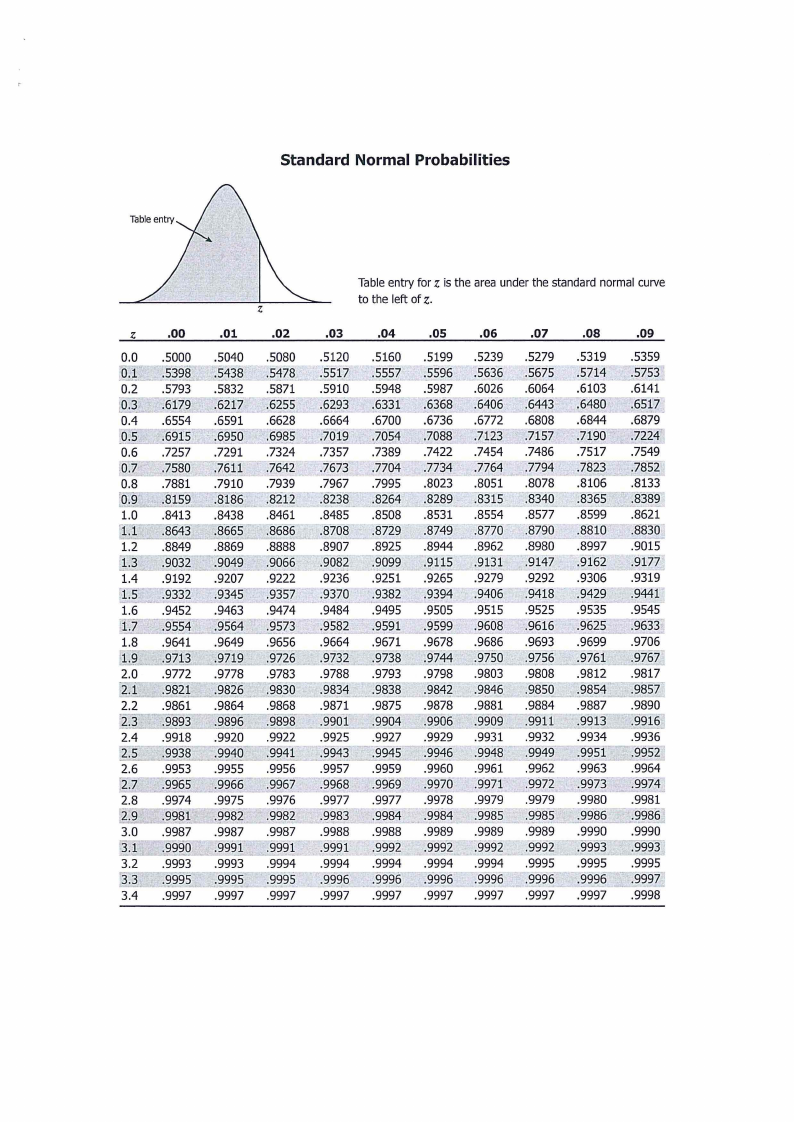
1. Z Table
This paper consists of 3 pages excluding this front page
 |
2 Page 2 |
▲back to top |

Question 1 [20 marks]
1.1 Briefly explain the following terminologies as they are applied in set theory and probability
theory.
(i) Set
[2]
(ii) Random experiment
[2]
(iii) Sample space
[2]
(iv) Event
[2]
(v) Independent events (say A and B)
[2]
1.2 Consider the sample space S = {coper, sodium, nitrogen, potassium, uranium, oxygen, zinc}
and the all elements are equiprobable, and further consider the following events:
A= {copper, sodium, zinc}, B = {sodium, nitrogen,potassium},
C = {oxygen}.
1.2.1 With reasons, state whether true or false that {A, B, C} is a partition of S.
[2]
1.2.2 Find the following probabilities:
(i) P(A)
[1]
(ii) P(A U B)
[2]
(iii) P(B - A)
[2]
(iv) P(B EBC) (hint: EBmeans symmetric difference)
[3]
Question 2 [25 marks]
2.1 To determine whether drinking alcoholic beverages has an effect on the bacteria that cause
ulcers, researchers developed the following table of the joint probabilities.
Number of alcoholic
Drink per Day
None
One
Two
:tvlorethan two
Ulcer
0.01
0.03
0.03
0.04
No Ulcer
0.22
0.19
0.32
0.16
(i) What is the proportion of people have ulcers?
[2]
(ii) What is the probability that someone has an ulcer or does not drink alcoholic
beverages?
[3]
(iii) If someone has an ulcer, what is the probability that he or she drinks alcoholic
beverages?
[5]
2.2 A rare disease exists with which ouly 1 iu 500 is affected. A test for the disease exists, but of
course it is not infallible. A correct positive result (patient actually has the disease) occurs
95% of the time, while a false positive result (patient does not have the disease) occurs 1%
of the time. If a randomly selected individual is tested and the result is positive, what is the
probability that the individual has the disease?
[5]
1
 |
3 Page 3 |
▲back to top |

2.3 A certain federal agency employs three consulting firms (A, B, and C) with probabilities
0.40, 0.35, and 0.25, respectively. From past experience it is known that the probability of
cost overruns for the firms are 0.05, 0.03, and 0.15, respectively. Suppose a cost overrun is
experienced by the agency.
(i) What is the probability that the consulting firm involved is company C?
[6]
(ii) What is the probability that the consulting firms involved is company A and B? [4]
Question 3 [30 marks]
3.1 The natural remedy echinacea is reputed to boost the immune system, which will reduce
the number of flu and colds. A six-month study was undertaken to determine whether the
remedy works. From the study, the following probability distribution of the number of res-
piratory infections per year (X) for echinacea users was produced.
2
3
4
p(x) 0.45 0.31 0.17 0.06 0.01
(i) Find is the expected number of respiratory infections among echinacea users?
[3]
(ii) Find the standard deviation of the expected number of respiratory infections among
echinacea users.
[5]
(iii) Find the cumulative distribution of X.
[5]
(iv) What is the median value of X?
[1]
3.2 A chemist measures the temperature of a solution in °C. The measurement is denoted by T,
and is normally distributed with mean 30°C and a standard deviation 2°C. The measurement
is converted to °F by the equation F = l.8T + 32. Then what is
(i) the mean value of F?
[2]
(ii) the median value of F?
[2]
(iii) the variance of F?
[2]
3.3 A cereal manufacturer is aware that the weight of the product in the box varies slightly
from box to box. In fact, considerable historical data have allowed the determination of the
density function that describes the probability structure for the weight (in ounces). Letting
X be the random variable weight, in ounces, the density function can be described as
82 if 23.75 < y < 26.25
f (y) = {
otherwise
Find:
(i)E(Y)
[3]
(ii) E(Y 2)
[3]
(iii) V ar(Y)
[2]
(iv) median of y (hint: First, find F(Y)).
[4]
2
 |
4 Page 4 |
▲back to top |

Question 4 [25 marks]
4.1 A certain type of tomato seed germinates 90% of time. A backyard farmer planted 10 seeds.
Find
(i) the probability that at most 3 seeds germinates,
[4]
(ii) the mean number of seeds that will germinate.
[2]
4.2 For a certain type of copper wire, it is known that, on the average, 1.S flaws occur per
millimeter. Assuming that the number of flaws is a Poisson random variable,
(i) what is the probability that no flaws occur in a certain portion of wire of length 5
millimeters?
[3]
(ii) what is the mean number of flaws in a portion of length 5 millimeters?
[2]
4.3 The width of bolts of fabric is normally distributed with mean 950 mm and standard devia-
tion 10 mm.
(i) What probability that a randomly chosen bolt has a width between 947 and 958 mm?[4]
(ii) What is the appropriate value for c such that a randomly chosen bolt has a width less
than c with probability 0.8531?
[5]
4.4 A random variable X has a meanµ= 10 and a variance a 2 = 4. Use Chebyshevs theorem
to find the value of the constant c such that P(IX - 1012::c) :$ 0.04
[5]
END OF QUESTION PAPER
3
 |
5 Page 5 |
▲back to top |
Standard Normal Probabilities
z
z .oo .01
-3.2 .0007
-3.1 .ooio
-3.0 .0013
-2.~ .0019
-2.8 .0026
-2.7 .0035
-2.6 .0047
,2.5 .0062
-2.4 .0082
-2.3 .0107
-2.2 .0139
-2.1 .0179
-2.0 .0228
..:..1,9 .6287
-1.8 .0359
-1.7 .0446
.0003
.0005
.0007
.0009
.0013
.0018
.0025
.0034
.0045
.0060
.0080
ill04
.0136
.0174
.0222
.0281
.0351
.0436
-1.2
.1131
-1.1 .1357 .1335
-1.0 .1587 .1562
-0.9 .1841 .1814
-0.8 .2119 .2090
-0.7 .2420 .2389
-0.6 .2743 .2709
-0.5 .3085 .3050
-0.4 .3446
.4168
.4562
-0.0
.4960
.02
.0003
.0005
.0006
.0009
.0013
.0018
.0024
.0033
.0044
.0059
.0078
.0102
.0132
.0170
.0217
.6274
.0344
.0427
.0526
.0643
.0778
.0934
.1112
.1314
.1539
.1788
.2061
.2358
.2676
.3015
.3372
.3745
.4129
.4522
.4920
Tableentry for z is the area under the standard normalcurve
to the left of z.
.03
.0003
.0004
.0006
.0009
.0012
·.0017
.0023
.0032
.0043
.00-57
.0075
]099
.0129
.0166
.0212
.0268
.0336
.0418
.0516
.0630
.0764
.0918
.1093
.1292
.1515
.1762
.2033
.2327
.2643
.2981
.3336
.3707
.4090
.4483
.4880
.04
.0003
.0004
.0006
.0008
.0012
.0016
.0023
.0031
.0041
.0055
.0073
.0096
.0125
.0162
.0207
.0262
.0329
.0409
.0505
.0618
.0749
.0901
.1075
.1271
.1492
.1736
.2005
.2296
.2611
.2946
.3300
.3669
.4052
.4443
.4840
.OS
.0003
.(l004
.0006
.0008
.0011
.0016
.0022
.0030
.0040
.0054
.0071
.0094
.0122
.0158
.0202
.0256
.0322
.0401
.0495
.0606
.0735
.0885
.1056
.1251
.. 1469
.1711
.1977
.2266
.2578
.2912
.3264
.3632
.4013
.4404
.4801
.06
.0003
.0004
.0006
.ono8
.0011
.0015
.0021
.0029
.0039
.0052
.0069
.009-1
.0119
.0154
.0197
.0250
.0314
.0392
.0485
.0594
.0721
.0869
.1038
.1230
.1446
.1685
.1949
.2236
.2546
-~~77
.3228
.3594
.3974
.4364
.4761
.07
.08
.0003 .0003
.0004 .6004
.0005 .0005
.0008--.0007
.0011 .0010
.0015 .0014
.0021 .0020
.0028 .0027
.0038 .0037
.0051 .0049
.0068 .0066
.0089 .0087
.0116 .0113
.0150 .0146
.0192 .0188
.0244 .0239
.0307 .0301
.0384 .0375
.0475 .0465
.0582 .0571
.0708 .0694
.0853 .0838
.1020 .1003
.1210 .1190
.1423 .1401
.16- 60 .1635
.1922 .1894
.2206 .2177
.2514 .2483
.2843 .2810
.3192 .3156
.3557 .3520
.3936 .3897
.4325 .4286
.4721 .4681
.09
.0002
.0003
.0005
.6007
.0010
.0014
.0019
.0026 1
.0036
.0048
.0064
.0084
.0110
.0143
.0183
.0233
.0294"
.0367
.0455
.0559
.0681
.0823
.0985
.1170
.1379
.1611
.1867
.2148
.2451
.2776
.3859
.4247
.4641
 |
6 Page 6 |
▲back to top |
Standard Normal Probabilities
z .00
0.0 .5000
_0_J._ ..5398
0.2
.6554
.6915
0.6 .7257
.0.7 .7580
0.8 .7881
10.9 .8159
1.0 .8413
1.1 .8643
1.2 .8849
1.3 .9032
·1.s 1.4 .9192
.9332
1.6 .9452
1.7 .9554
1.8 .9641
1.9 .9713
2.0 .9772
2.1 .9821
2.2 .9861
2.3 .9893
2.4 .9918
2.5 .9938
2.6 .9953
2.7 .9965
2.8 .9974
12.9 .9981
3.0 .9987
.9990
.9993
3.4 .9997
z
.01
.02
.5040
-~438
.5832
.6217
.6591
.6950
.7291
.7611
.7910
.8186
.8438
.8665
.8869
.9049
.9207
.9345
.9463
.9564
.9649
.9719
.9778
.9826
.9864
.9896
.9920
.9940
.9955
.9966
.5080
.5478
.5871
.6255
.6628
.6985
.7324
.7642
.7939
.8212
.8461
.8686
.8888
.9066
.9222
.9357
.9474
.9573
.9656
.9?2,6
.9783
.9830
.9868
.9898
.9922
.9941
.9956
.9967
.9976
.9993
.9995
.9997
.9994
.9995
.9997
z Table entry for is the area under the standard normal curve
to the left of z.
.03
.5120
_d5i7
.5910
.6293
.6664
.7019
.7357
.7673
.7967
.8238
.8485
.8708
.8907
.9082
.9236
.9370
.9484
.9582
.9664
.9732
.9788
.9834
.9871
.9901
.9925
.9943
.9957
.9968
.9977
.9983
.9988
.9991
.9994
.9996
.9997
.04
.5160
.5557
.5948
.6331
.6700
.7054
.7389
.7704
.7995
.8264
.8508
.8729
.8925
.9099
.9251
.9382
.9495
.9591
.9671
.9738
.9793
.9838
.9875
.9904
.9927
.9945
.9959
.9969
.9977
.9984
.9988
.9992
.9994
.9996
.9997
.OS
.5199
.5596
.5987
.6368
.6736
.7088
.7422
.7734
.8023
.8289
.8531
.8749
.8944
.9115
.9265
.9394
.9505
.9599
.9678
.9744
.9798
.9842
.9878
.9906
.9929
.9.946
.9960
.9970
.9978
.9984
.9989
.999-2
.9994
.9996
.9997
.06
.5239
.5636
.6026
.640-6
.6772
.7123
.7454
.7764
.8051
.8315
.8554
.8)70
.8962
.9131
.9279
.9406
.9515
.9608
.9686
.9750
.9803
.9846
.9881
.9909
.9931
.9948
.9961
.9971
.9979
.9985
.9989
.9992
.9994
.9996
.9997
.07
.5279
.5675
.6064
.6443
.6808
.7157
.7486
.7794
.8078
.8340
.8577
.8790
.8980
.9147
.9292
.9418
.9525
.9616
.9693
.9756
.9808
.9850
.9884
.9962
.9972
.9979
.9985
.9989
.9992
.9995
.9996
.9997
.08
.5319
.5714
.6103
.6480
.6844
.7190
.7517
.7823
.8106
.8365
.8599
.8810
.8997
.9162
.9306
.9429
.9535
.9625
.9699
.9761
.9812
.9854
.9887
.9913
.9990
.9993
.9995
.9996
.9997
.09
.5359
.5753
.6141
.6517
.6879
.7224
.7549
.7852
.8133
.ff389
.8621
.8830
.9015
.9177
.9319
.9441
.9545
.9633
.9706
.9767
.9964
.9974
.9981
.9986
.9990
.9993
.9995
.9997
.9998





