 |
AOR802S - APPLIED OPERATIONS RESEARCH - 2ND OPP - JANUARY 2025 |
 |
1 Page 1 |
▲back to top |

nAmlBIA UnlVERSITY
OF SCIEnCEAnDTECHnOLOGY
FacultoyfHealthN, atural
ResourcaensdApplied
Sciences
Schoool f NaturalandApplied
Sciences
Departmentof Mathematics,
StatisticsandActuarialScience
13JacksonKaujeuaStreet T: +264612072913
PrivateBag13388
E: msas@nust.na
Windhoek
W: www.nust.na
NAMIBIA
QUALIFICATIONS: BACHELORof SCIENCEHONOURS IN APPLIEDMATHEMATICS
BACHELORof SCIENCEHONOURS IN APPLIEDSTATISTICS
QUALIFICATION CODES: 0SBSMH, 0SBSSH
LEVEL:8
COURSE: APPLIEDOPERATIONSRESEARCH
DATE: JANUARY 2025
DURATION: 3 HOURS
COURSECODE: AOR802S
SESSION: 1
MARKS: 155 (To be converted to 100%)
SECONDOPPORTUNITY/SUPPLEMENTARY:EXAMINATION QUESTION PAPER
EXAMINER:
MODERATOR:
Prof Sunday A. Reju
Prof O/uwole D. Makinde
INSTRUCTIONS
1. Answer all questions on the separate answer sheet.
2. Please write neatly and legibly.
3. Do not use the left side margin of the exam paper. This must be allowed for the
examiner.
4. No books, notes and other additional aids are allowed.
5. Mark all answers clearly with their respective question numbers.
6. Use of COMMA is NOT ALLOWED for a DECIMAL POINT.
PERMISSIBLEMATERIALS
1. Non-Programmable Calculator
ATTACHMENTS
NONE
This paper consists of 4 pages including this front page.
 |
2 Page 2 |
▲back to top |

QUESTION 1 [26 MARKS]
A construction company is bidding for the building of a new College Hostel or its Classroom
Block or a combination of both. The construction company must submit a bid proposal, which
costs money to prepare, and there are no guarantees that it will be awarded the contract. If
the company bids on the Hostel, it has a 35% chance of getting the contract, and it expects to
make $162,000 net profit. However, if the company does not get the contract, it loses
$11,500. If the company bids on the Classroom Block, there is a 25% chance of getting the
contract, and it would net $140,000 in profit. However, if the company does not get the
contract, it will lose $5,750.
(a) What should the construction company do?
(10 Marks)
(b) How sensitive to the estimate of the probability of the award of a contract-is the
decision (i):
• in either to build the Hostel or the Classroom Block?
(6.5 Marks)
• to the net profit for each case, if awarded the contract?
(9.5 Marks)
QUESTION 2 [63 MARKS]
(a) Using the linear programming problem (LPP) approach in obtaining the solution of the
game with the following payoff matrix:
Il 1 -1
-3 0
0 -2
-2 -3
Obtain the optimal mixed strategies for the two players and the value of the game,
discussing your solutions.
(47 Marks)
(b) Consider the following Queueing System Data:
Queueing System for 2 Servers with Balking and Reneging
Balk if queue length is or
Renege if waiting time
Start Time
Close Time
I 09:00
09:20
lnterarrival Time Probability Distribution
exceeds
DJ
I exceeds
2 minutes
Service Time Probability Distribution
Lower
Upper
lnterarrival
Lower Upper Service
Probability Bound
Bound
Time
Probability
Bound Bound
Time
(min)
(min)
0.45
0
0.45
1
0.3
0
0.3
2
0.25
0.45
0.7
2
0.35
0.3
0.65
4
0.1
0.7
0.8
2
0.35
0.65
1
6
0.2
0.8
1
1
Obtain a Simulation Table for 5 customers using the following header:
(16 Marks)
CourseName(AOR802S}
2ndOpportunity January2025
2
 |
3 Page 3 |
▲back to top |
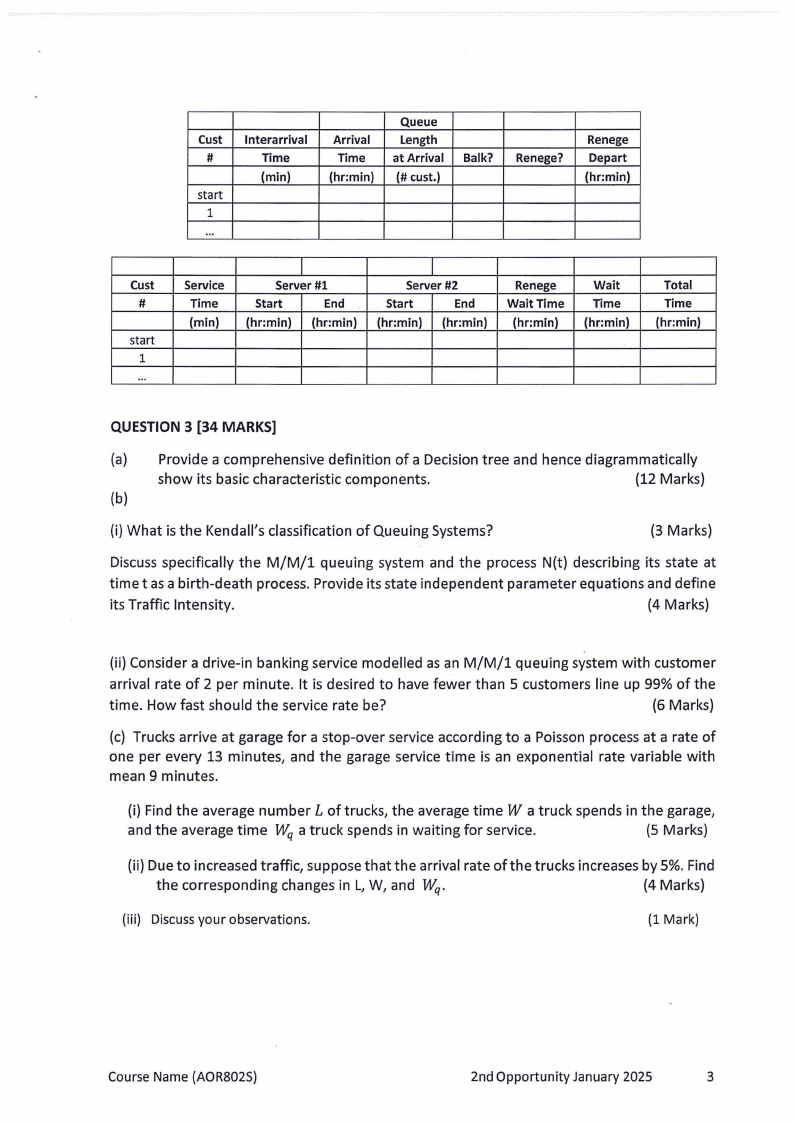
Cust
#
start
1
...
lnterarrival
Time
(min)
Arrival
Time
(hr:min)
Queue
Length
at Arrival
(# cust.)
Balk?
Renege?
Renege
Depart
(hr:min)
Cust
#
start
1
...
Service
Time
(min)
Server #1
Start
Enc:I
(hr:min) (hr:min)
Server #2
Start
End
(hr:min) (hr:min)
Renege
Wait Time
(hr:min)
Wait
Time
(hr:min)
Total
Time
(hr:min)
QUESTION 3 (34 MARKS]
(a) Provide a comprehensive definition of a Decision tree and hence diagrammatically
show its basic characteristic components.
{12 Marks)
(b)
(i) What is the Kendall's classification of Queuing Systems?
(3 Marks)
Discuss specifically the M/M/1 queuing system and the process N(t) describing its state at
time t as a birth-death process. Provide its state independent parameter equations and define
its Traffic Intensity.
(4 Marks)
(ii) Consider a drive-in banking service modelled as an M/M/1 queuing system with customer
arrival rate of 2 per minute. It is desired to have fewer than 5 customers line up 99% of the
time. How fast should the service rate be?
(6 Marks)
(c) Trucks arrive at garage for a stop-over service according to a Poisson process at a rate of
one per every 13 minutes, and the garage service time is an exponential rate variable with
mean 9 minutes.
(i) Find the average number L of trucks, the average time W a truck spends in the garage,
and the average time Wq a truck spends in waiting for service.
(5 Marks)
(ii) Due to increased traffic, suppose that the arrival rate of the trucks increases by 5%. Find
the corresponding changes in L, W, and Wq.
(4 Marks)
(iii) Discuss your observations.
(1 Mark)
Course Name (AOR802S)
2nd Opportunity January 2025
3
 |
4 Page 4 |
▲back to top |
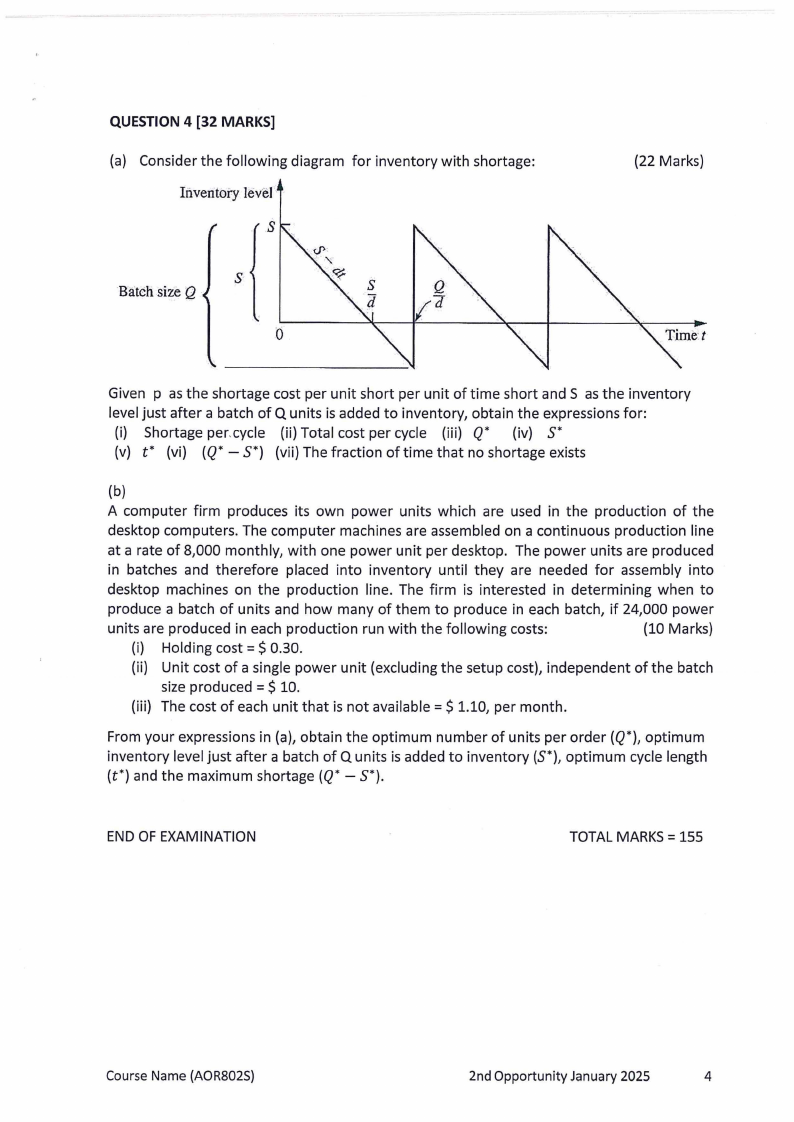
QUESTION 4 [32 MARKS]
(a) Consider the following diagram for inventory with shortage:
Inventory level
s
s
"Batchsize Q
(22 Marks)
Given p as the shortage cost per unit short per unit of time short and S as the inventory
level just after a batch of Q units is added to inventory, obtain the expressions for:
(i) Shortage per.cycle (ii) Total cost per cycle (iii) Q* (iv) S*
(v) t* (vi) (Q* - S*) (vii) The fraction of time that no shortage exists
(b)
A computer firm produces its own power units which are used in the production of the
desktop computers. The computer machines are assembled on a continuous production line
at a rate of 8,000 monthly, with one power unit per desktop. The power units are produced
in batches and therefore placed into inventory until they are needed for assembly into
desktop machines on the production line. The firm is interested in determining when to
produce a batch of units and how many of them to produce in each batch, if 24,000 power
units are produced in each production run with the following costs:
(10 Marks)
(i) Holding cost=$ 0.30.
(ii) Unit cost of a single power unit (excluding the setup cost), independent of the batch
size produced = $ 10.
(iii) The cost of each unit that is not available = $ 1.10, per month.
From your expressions in (a), obtain the optimum number of units per order (Q*), optimum
inventory level just after a batch of Q units is added to inventory (S*), optimum cycle length
(t*) and the maximum shortage (Q* - S*).
END OF EXAMINATION
TOTALMARKS= 155
Course Name (AOR802S)
2nd Opportunity January 2025
4





