 |
SIN502S - STATISTICAL INFERENCE 1 - 2ND OPP - JAN 2023 |
|
|
1 Page 1 |
▲back to top |
n Am I BI A u n IVER
s I TY
0 F SC I En CE An D TECH n O LO G Y
Faculty of Health, Natural Resources and Applied Sciences
Department of Mathematics and Statistics
QUALIFICATIONS:BACHELOROF SCIENCESIN APPLIEDMATHEMATICSAND STATISTICS
QUALIFICATION CODE: 07BSAM
LEVEL: 5
COURSE:STATISTICALINFERENCE1
COURSECODE: SIN502S
DATE:JANUARY2023
SESSION: 1
DURATION: 3 HOURS
MARKS: 100
SUPPLEMENTARY/SECOND OPPORTUNITYEXAMINATION QUESTION PAPER
EXAMINER(S)
MR. EM. MWAHI, DR.D. NTIRAMPEBA
MODERATOR:
DR.J. ONG'ALA
THIS QUESTION PAPERCONSISTSOF 6 PAGES
(Including this front page)
INSTRUCTIONS
1. Answer all the questions and number your solutions correctly.
2. Question 1 of this question paper entails multiple choice questions with options A to
D. Write down the letter corresponding to the best option for each question.
3. For Question 2, 3 & 4 you are required to show clearly all the steps used in the
calculations.
4. All written work MUST be done in blue or black ink.
5. Untidy/ illegible work will attract no marks.
PERMISSIBLEMATERIALS
1. Non-Programmable Calculator without the cover
ATTACHMENTS
Z-table, t-table, Chi-square table, Mann-Whitney U table and the F-table
1
|
|
2 Page 2 |
▲back to top |
QUESTION 1 [20 MARKS]
Write down the letter corresponding to the best answer for each question.
1.1 When the population is divided into mutually exclusive sets, and then a simple random
sample is drawn from each set, this is called:
[2]
A. Simple random sampling.
B. Stratified random sampling.
C. Cluster random sampling.
D. Systematic random sampling.
1.2 A marketing research firm divides the population of a state into geographic areas, and
randomly selects some of the areas and takes a simple random sample of each
selected area. This is an example of a
[2]
A. Cluster random sample
B. Systematic random sample
C. Simple random sample
D. Stratified random sample.
1.3 The use of the laws of probability to make inferences and draw statistical conclusions
about populations based on sample data is referred to as ___ _
[2]
A. Descriptive statistics
B. Inferential statistics
C. Sample statistics
D. Population statistics
1.4 A sample of size 55 is drawn from a slightly skewed distribution. What is the
approximate shape of the sampling distribution?
[2]
A. Skewed Distribution
C. Normal Distribution
B. Chi-square Distribution
D. Uniform Distribution
1.5 What should be the value of Z used in a 92% confidence interval?
[2]
A. 2.70
B. 1.75
C. 1.81
D.1.89
2
|
|
3 Page 3 |
▲back to top |
1.6 A researcher is studying students' behaviour in colleges in California. She takes a
sample of 400 students from 10 colleges. The average age of these 400 students in
California is?
[2]
A. A statistic.
B. A parameter.
C. The median.
D. A population.
1.7 The standard deviation of a normal population is 10. You take a sample of 25 items
from this population and compute a 95% confidence interval. In order to compute the
confidence interval, you will use:
[2]
A. The t table because the degrees of freedom will be 24.
B. The t table because the sample standard deviation is known.
C. The z table because the population standard deviation is known.
D. The z table because the sample size is small.
1.8 If in a random sample of 600 items, 132 are found to be defective. If the null
hypothesis is that 21% of the items in the population are defective, what is the value
of the test statistic?
[2]
A. 0.22
B. 1
C. 0.60
D. 0.21
1.9 A 91% confidence interval for population proportion is 32.4% to 47.6%, the value of
sample proportion is:
[2]
A.40%
B. 32.4%
C. 47.6%
D. 80%
1.10 A null hypothesis was rejected at level alpha=0.10. What will be the result of the test
at level alpha=0.05?
[2]
A. Reject Ho
B. Fail to Reject Ho
C. No conclusion can be made
D. Reject Ha
3
|
|
4 Page 4 |
▲back to top |
QUESTION 2 [56 MARKS]
2.1 The personnel department of a large corporation wants to estimate the family dental
expenses of its employees to determine the feasibility of providing dental insurance
plan. A random sample of 20 employees reveals the following family dental expenses
{in N$) for the past year.
16 20 13
19 24 22 18 18
15 20
20 21 21 18
20 18 20 15 20
18
2.1.1 Find the mean point estimate for the employees' dental expenditure in the
past year.
[3]
2.1.2 Compute a 95% confidence interval for the true population mean in the
employees' dental expenditure.
[6]
2.2 Suppose the time it takes a randomly chosen clerical worker in an office to type and
send a standard letter of recommendation has a normal distribution. The population
mean is 10.5 minutes and the standard deviation of 3 minutes. You take a random
sample of 50 clerical workers and measure their times.
2.2.1 What is the probability that their average time is more than 570 seconds?[6]
2.2.2 What is the probability that their average time is between 9.5 minutes and
11 minutes?
[4]
4
|
|
5 Page 5 |
▲back to top |
2.3 A study was conducted to investigate the effectiveness of hypnotism in reducing
pain. Eight subjects were randomly selected and their sensory measurements before
and after taking hypnotism are shown in the table below.
Before 6.6
6.5
9.0
10.3
11.3
8.1
6.3
11.6
After
6.8
2.4
7.4
8.5
8.1
6.1
3.4
2.0
At a 5% level of significance, from the sample data, is there sufficient evidence to
conclude that the sensory measurements, on average, are higher after hypnotism?
Assume that the population is normally distributed.
[10]
2.4 With individual lines at its various windows, a post-office is interested in the standard
deviation for normally distributed waiting times for customers on Friday. The post-
office experiments with a single main waiting line and find that for a random sample
of 25 customers, the waiting times for customers have a variance of 12.25 minutes.
2.4.1 With a significance level of 5%, construct a confidence interval estimate for the
variance waiting times of all customers at this post-office on a Friday. [6]
2.4.2 Assuming that the estimated population variance at this post-office is 51.84
minutes-and the population is normally distributed, is there evidence at 1%
level of significance to conclude that a single main waiting line causes lower
variation among waiting times?
[7]
2.5 The contingency table below shows a random sample of 439 U. S adults who were
questioned regarding their political affiliation and opinion on a tax reform bill.
Political Affiliation
Democrat
Republican
Favor
138
83
Opinion on Tax Reform
Indifferent
64
84
Oppose
64
6
Test if the political affiliation and their opinion on a tax reform bill are dependent at a
5% level of significance.
[14]
5
|
|
6 Page 6 |
▲back to top |
QUESTION 3 [24 MARKS]
3.1 Someone has told you that there is no difference in abstract reasoning between men
and women. You are sceptical, so you decide to test this idea. You randomly select
eight adult men and eight adult women living in your hometown and administer an
abstract reasoning test. A higher score reflects better abstract reasoning abilities. You
obtain the following scores:
Men
Women
70
86
60
92
82
50
74
94
81
80
50
95
93
65
90
75
At the 5% level of significance, use the Mann-Whitney U test to test if there is a
difference in scores between the two groups.
[10]
3.2 A partially complete ANOVA table for a completely randomised design is shown:
Source of
variation
Between (treat)
Within (error)
Total
Degree of
Sum of Square Mean Square
freedom (df)
24
(SS)
.................
(MS)
14.46
30
................ ...........
...............
505.3
F-stat
...........
3.2.1 Copy and Complete the ANOVA table
[S]
3.2.2 How many treatments are involved in the experiment?
[2]
3.2.3 Do the data provide enough evidence to indicate a difference between the population
means? Carry out an appropriate test using alpha= 0.05.
[S]
3.2.4 Based on your conclusion in 3.2.3, is it appropriate to do a post hoc test? Justify your
answer.
[2]
END OF EXAMINATION
6
|
|
7 Page 7 |
▲back to top |
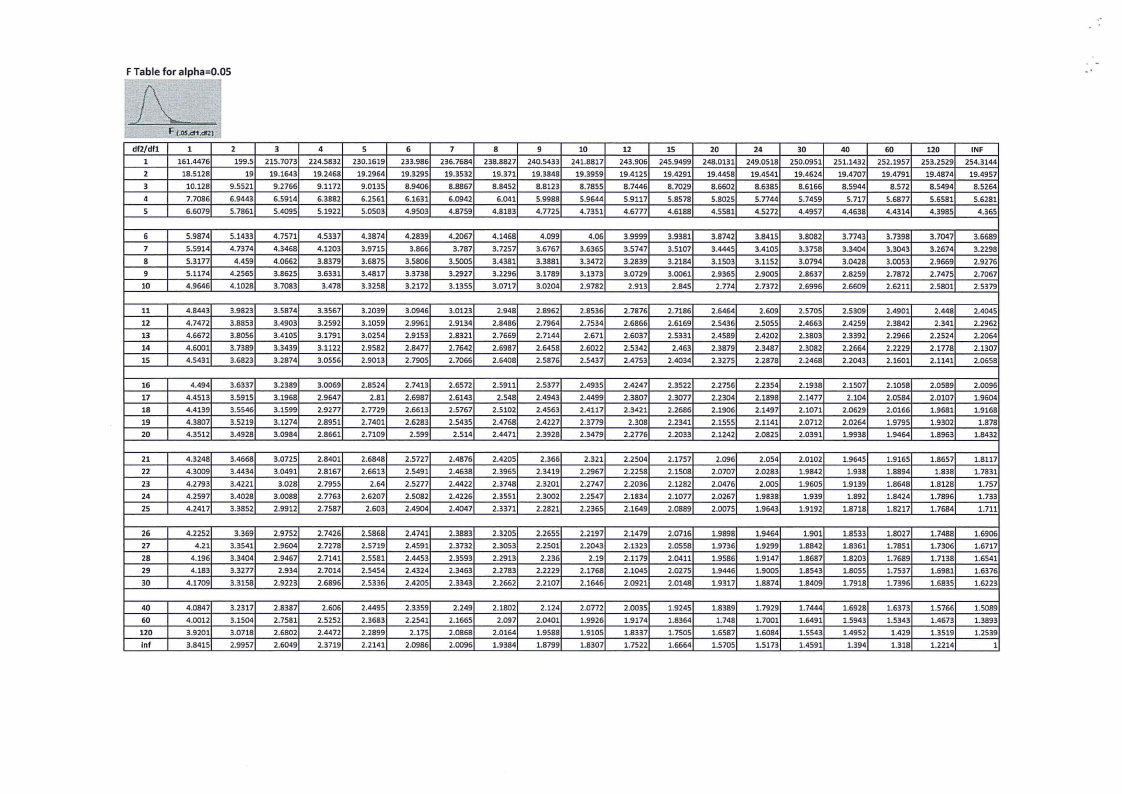
APPENDIX C: The Standard Normal Distribution
APPENDIX D: The t-distribution
-
~.-..
·~· ·.°:_':
:::---::.:~~::=~~~:::~: :~. {r 1t:.:.-.•. ;rttr " -·-- -·--i: l:°.,ii~?. 0.00 0.01 0.02 0.03
~-o ;0.0000 0.0040 'o.0080[~,o\\~o ![0.0160!0.0199
~:~7:,_ 0.08
'.'°.·°.~79fo.0319 :'o.03s9
1
:~::
_ ·; t:.~:::·-·:--1-::-~:~:!{r{·i·:··
··-·J··,~•·:•~:·;:·:_:t:_!: _:::t:·.:i::~:,:;~!:··:it~~!~::-·.:::!::~;::t:::
dl\\p [o:~o:-::1[ -0.25-:J 0.10
J .. ~:?~ ~.025 "···O·:~l.. 0.005
::0,32492-0J. !1.o~;c3:i0o17o6_i8_l4}-6.:313752]12:10620-:i3!.~~?5~_
-~2 ~-.;;::;~;;~:\\::;.;:;;:__~-_t:;::J:~.;:54:07:0:.._:.:;~.~091 !'12.9240 .,
....·.:.in i:0:1406.9..71ri:s:i3206\\i:131841 ':2.7764s·.·1· j3.74695[4.604o9 ,8.6103
ro:i-iii5 o.1iisa··:·~:ii~··§:r§_.2iiii~i )ij:20.~:'~ii:iiiiiii :'ii.2i·n-]-'.oji~?- :~I21w 'p:2224
·············j[~J,7[i2:~6~??788:4..
:;:i.36493 :1:i,0~2.1J~:6_.8688
0.2291 ··o.2324:[o.2357ilo.2389. :·o.2422io:2454 i'o:2486-,-0.2517:'0.2549
:fo}f~; .i ,0:3611...:.0.2642 :1~.267-3'J@)'.?1:~~.27~4 0,2764
:bjii~..::.~.,~8!.>...2.
0.8
:.~:::;t:;:;:~·;·!·~··:::;: ··;t:~;~::~Ii·::·J:·~~::i:1:~~~::·m.·-·:·~::{::······- 0.9
,[i::~:···.····.··· :~::::··
6 0:2648_35J!0.7175~[1.439756. -· -- J2 .4. 4691 1'3,:1~~~~--i~7074~3".J.~.9588
7 ,o:2ii:iiG'ii!o.11114211.414924'[i.894579 !2.36462 ::2.99795 ]!349948 Ts:;;o;,g
8 '0.261921Ji?:7-~~3.~..!J.[;:3?~!5...'.'l.ll5!l548 :fi.30600 Ji~~9646~,i~:35539 5.0413
9 Jo.260955 i!o:7027221\\383029 ,_____ :j2.26216.112.82144 '!3.24984 i 4.7809
1.0 !'o:34jx 0}438 :a:34~1_;~.348_5 :,0-~508!o.353-1 0.3554 l'o:3~7~_:[0.35.9..9)i:3621
=: 1.1
:}:~.:.!-.:.·.:·.::.·:::!!:t.·~-::-;:~!:~!~~f'l!!~t:-;-_-:-:~i·:!:;:::!:·-:.:!~:t~l;-··· 1.2
:·o.3830
10 '0.260185i:o.6998172:1.312184 '1.812461 :!2.22814 .i.'2.7Gl7-77t,3.-16927--"4.5869
[······11 . '.~.~5~55']6'~.69;_~~jf~:~6;,;;~~~1.79588;~_i:i:2~9~--J2.118~t ~ii~;o~~.t• ;4.4370
.:-::-i2'7 :?,259?33J:o:695483J[i.:i~6i1:1::-':,:ia22ss::2:11aai T2.68100-·:::i:05454·:·4··:·3·17.~......
.1..:.~.j'o,4032 0.4049 ,_0:406~:p,'.'_0_~H3o_,409-90-,4115 :p.~131 0.4.14.?::0,'.'.1~3
..1-4__,o_.419.2.....0...4207·.·.'.·0·,422-2··-•'.0.42_3_6:_:o.42_5_1_'0.426_5_j 0.4279_'_0.4292__''_o.430_6_. ..
---1-3--··-·
···-··-··-·-··-····
'----····••--·-••- ..•...........
,1.350171"1.770933
...................._.;.,..,..._..,.
j2.J6037
;!2.65031 ·-=~=
,4....2.._2..0,,8_,,._,,,,
14 'o.25821:i°::·o.692417i'l.345030 ,,1.761310·ni.1«79 ..::2.62449 '2.97684 '4.1405
! - 1,5
.........
.'o. .4332
OA345 0.4357 :0,4370-Ho.4382i 0.4394.. .o.44:06.
Jp::i429 '.?:4 .
1.6 0.4452 0.4463 ·o.44-7-4-· -- :(),~95 0.4505 j 0.4515_ i~.:.45_2!~p.4535__ ::0,4545
15 0.2578~.J~o.:~?.l_l.?.?·.•i.34060f_:::1:753050112:13145112.60248!!2.94671 14.0728
16 0.25_7599~=':ci:iiiio•~:13.i3_3675(Jii:745884 :J;1u991- ,;2.58~_9_ :~~078 14.0150
1.7 ,0.4554 0.4564 '.0:~~.7.i.!30.4~::i·;~'0:.~~91 0.4599_.;0',:6.o~:-g_::4616 \\~.:4..~?:~o-.4633
17 :o.25734:7:i:?·68919..5.E333.J_7_f9l_!:73.!l(;0j72.10982' Jl:isGG\\91.:8i9.823 !3.9651
1.8 jo._4641 'o.4649 ·'ii:4656 .\\0A664 jf0.4671 0.4678 i'o.diiiic; 0.4693 :idiiii9 o.4706
;~,.~.±~~. fo:;;;~a 1,9 _i,0.4713 'o.4719 :o.4726 10,4732.::o.4738j 0.4744
_o.7456 ;'0.4761 i°0.4767
2.0 Tci:47··7·2'·c·i·:41··1· .f f4iaa :ro:~f~:i 0.4798 i'o.4803 °0.4808i;a:4liii ::o:4iii7
2.1 :o.4821 ,~,~26 ..:a.483_0-,ro~4834-i;a.4838 0.4842 i0.4846 '0.4850 ''.o.4854,°0.4857
···.·.-.·:·.,:.·:.·.;-.:.·::1~:.i:;:.;:··;;::~:::~:!-·.·.:.·~·:·:::·.·:~;:;·:!~::r::·-·~:-·:·:·.:···~··:1;:::;
20 °io.25674J3-f:::]::t:i::_~{c',iJ;i~::;~:~::::-:;:;::.-::,:.;:_::~::I :
2.2
..;.~.
2.3
0.4861 o.4864 :o.4868 "0.4871 ::o.4875 0.4878 '0.4881 ,0.4884 i0.4887 p.4890
•0.4893 ·o.4896 'o.4898 •'0.4901 ;:o.4904 0.4906-·i~0....490,.9·.··-·-··.·0.·..·..4i.:..9..1...1.....:.:.0...,.4...9..1...3....'.o...:..4...!..i.i..6.
2:::' .•; 0.4918. 0.4920 '0.4922 \\0.4925 :io..i921 ,0.4929 0.4931 :0,4932 :o.4934 :o.4936
22 __0.25643J2[~.6~5~0~ -~~-
'----~-:.:-:'.?:2.~~~...?J..o1. .685306
·:2.07387 .2.50832 :'~.81876 i3.7921
·-____,:206866 ,;2.49?~!-::=::[~?7~-1~3.7676
2.5 f 0.4938 0.4940 0.4941 110.:194f3o.4945
0.4948 ·0,4949 )l.4951 :o.4952
~:0.256173 · i,o.6848.5. 0Jl.317836 ··-----·-·--)-2-.06390 !j2,49216 :j2.79694 '.3.:.?..~..5.:1
2.6 ;0.4953 0.4955 :o.4956 'fo,4957 io,4959
·10r-·.·4···.9..·.6.• 2 ;o.4963 ).4964
_25___ :o.25(;_()6]0!~.6~o~ ;1.31634.5,!1-7?8141'j2.05954 !:2.4851_._i~:,2.78744 ; 3.7251
2.7 -:c0.4965 0.4966 _0.4~~7)0,4968 ,'0.4969 i.0.4970 i0.4971 :0,4972
........:,-..0.4974
2.8 '0.4974 0.4975 ·o.4976 .,0.497_?__;:~.49707.4978
-0.4979
'.0.4981
2.9 0.4981 0.4982
· ,:o:4984·!'a:4984 ,o.,iiiiis ::o'.~9._8}.o~.4986 .I-i9s6
'.il~::::::~:[:~;]t:;::~!~~!~~:~:.:~~---,,;;:;~i: 2~-----;o:2s~9j5~0..684~~ J_t:3i49_72-·1--.7-05618-;2.055~-- )~~7863-- :!2.778_7_1_''i7066
27-- - '0~2ssssa
'.!idi2i·i·i·-i:·,·i:11068 :·:::::
3,0 0.4987 0.4987 ).~9.8? )'.~9.8.~)'.4988 J~:498?. :.o:4989-'.'ii:i9.~9~!iii4990''.0.4990
J[i:3.!1.~~ 29 ,;0.255684J:o.683..~
;:!,699121 ·12.04s2:i )[2:~~?o~ '[~?~~39··]·:·J·:·t·i.s94
30
}--~1.~i~- - ]'.?:~8.2.?.5...~
--ar;,697~~!1~·?4227·····:r2457~-::i.7500- 0 '3.6460
inf :o.253347. 
APPENDIX E: The Chi-Square Distribution
t~':~,'.t :d~p t. .995
.990
.950 L .9oo ;:
H_ .25o T :100 .o5o_:: .025 '.0_1_"0·._.._o._os
j-0.000J1l6~~o~D'!!l08._0039,3:0.0157:9:0.10153
:l!:~2~'132..:?.7..o?.5.".}~8li451_4o6i:i8:9fii:634!9:07.87944
]ii:ijo6_4: ·001003:ioioio
,:02101T2os1s3~=:1;:~Gti'1ii12sii
"s99146n1.3m6 :'921034bo59663
3 !0?1J:1:~j:ll~~i-jlo,_21]"5?8i~siiis:·•to:-s~3:r7;:2Jisi ,,,,,,,,,,,,,,
4
'o:~911.i"J~da~2Jo?l07'2ii:0636E2~22sr;"
5
·o.......5.....5....4....3-,~'0'··o···.·8····3···1···2·····1····1···.··1- 454·3,1.610··3··11::·2-··.- 67460
,l{t::ft: :,:~i·::~:lt::!f}:: '/057573::o.872019,f. L---~··· jj~,i..!:i-:·6353n18i:i:2cw,.1,·•13:i::. i~~
:t:!~i-::::::;:
l :H! J
,:
frlII:l:lstI~iltI:::::;:ltlilli!l:!I:I~!;I!I};i};_:zr:
9 '1.73493;2087-9•-0··-'--·-2---:-1- 00.:.1i·'•ii33251J1~:1~_161:S:iiiiiiiii
· ='•··•·····•·'
:::•:::-:•::t::·:;:-~::f~:::;_:_;-:;·:::i:;::::~:-:•-l:_::.;:i_::o:::-::::::::::::;:::;-::::::-:1:::~-:::~:::~::
:~-~3-~~ 12.J3.07382:_~51oiiJt~03?~_:i:22w::i")j53_1?_3.B_:°[.!,J,._,:~-~-3.2..::fi~~~54~;:j~1L8052469i0~:7~533366_GJ,26'2'2186.2!l97952
13 !356503J 4.1069_2;;~0~~75.·::~:~i9t1.18.6:~1-!~;~9.-2990l7[ii::i397~f1.59B391-:ii'i[i2.a2i:i~9~j 203f!473560'i27.6289B.82159:47
'!562873:657063 '
,.,''
~~...J i_.~.~. .~.?92_fl~:.~-.~..:~.1..~?.-.?~~;7--2~~4-~_-_-._~-_~-:~G76
1116:[,s5i:..6292712ll2i6a.14202717.-6i,'G.79,5o6i~41:,;79896~711~_'57_.:6[91301,02825419:i2_:7-9·1--9-3,[iG1'2_0j34B8l8868/2476904)21:58711rl0\\19101
i1i9i :'6G.8.24634987:[0/1i:;0:i12~1~i'"!1iiil2:9,3o06755i2:~1:03.9m0o41,·6[:1;10,.58560'1'91.9[:1_441.35,6627H0~[102i'1?ii~'.3333717:926025;.,721_71_:8[:[_21625019~.28~09~341>,523780~.61?433',05[':33i21._8.5_253~36\\_:J3G8_.1;i'!9_30~884.75_8._282_60_5.~_1![~.715645
20j.43384Tii2cio:;o
:t5.4517'!719.337'41323.827'!6298.411'91831.410i'4334_169[6:317,566i2339.99685
_2_1j_8.0336J5:_8:8.__9._:71210?·?~;2.i..?1?-?.~13_1;[1_j3_21~3_~_~89_6:?[20,33723jj2~::9!32497.6815)0!392.670j5[375.478J8[38R?3_.2!.:.~__11.?,40106
22':.8,6427.2954-- 24•9,1,.10·.••9-· 82· i,3,-,12-·2- .3380!; 14. .04.1p·4·:19-·7-·.-2-··3·9,::6,·221-.3--3--7;;0;:24..6.0392::370,813::2;;38. 3,.92. 4:,4:,·3.46-.7.80,•7,.410.289;i,3:462.79565
:;l::::::t:;:.::.~::1::[::i;:;:;:~:::::t;i\\;;:~i:::[:;.;;:J:f~:f:::~:[;;::;::::;:;;.:::;:~:;:;:;;: ::
'_.!S}l?,519.~151].523:9;183.l_l?'.!~4..6ll41•:16.4731i4l91.9393i244.3365'!929.3388j354_381,[5397:~~2~8)'40.64647!:4!i44.63912471809
26 --·;-;·16024,.12198:1151384319,1053791,:6172918280, 84343>533646304345.7!35.563''1378.88514.{41.9i4253.167416i48B.28988
·_27__i 1_1.00!_1529.8785o'i14.57338·1,1168'.1.is_-113491020-1-.:7i494:1026.33_6:3!431.52_8\\3461.74__:1_12420.11321_::43.19451.J:46.96294__!'49.64492
;za · 29J!::1132..;162;:1i:l1:;1iJ54:i:.2s566'.14::151.}5;0i;i34;o1f;a0:;1~;161~io72i_lal,F[i1i'i9ii:i1~_6!il:2_i:(;2:s4~6~6:s~;i9,ii_i.a2:i.31ij_i~J3i3.:i!]i:3_:3i~n2.0:269i21Jo'13•1:iii99;f1.05897:,2::4472_.15.5363f97171541.J2[2424ji9.:\\4~46985027878.79_8~i8/~5J2!..3~3~59692338
30,'l3~78Gii114:_?:~~7~.9i±'1j?G:9i6i~2_0:si:i2:2~ ~~7::{~ii;ii~~:!~~9974:40.256:0[42_737, 2l?l•!G9792.4)50.l~~9l:25~~1?.j6
|
|
9 Page 9 |
▲back to top |
•...
Critical Values of the Mann-Whitney U
(Two-Tailed Testing)
n2 a
3
4
5
6
7
8
n,
9 10 11 12 13 14 15 16 17 18 19 20
3
.05
.01
--
--
0
0
0
0
1
0
I
0
2
0
2
0
3
0
3
0
4
I
4
1
5
I
5
2
6
2
6
2
7
2
7
3
8
3
4
.05
.01
--
--
0
--
I
0
2
0
3
0
4
I
4
I
5
2
6
2
7
3
8
3
9
4
10 11 I I 12 13 14
556678
5
.05
.01
0
--
1
--
2
0
3
I
5
I
6
2
7
3
8
4
9
5
11 12 13 14 15 17 18 19 20
6 7 7 8 9 IO 11 12 13
6
.05
.01
I
--
2
0
3
I
5
2
6
3
8 10 11 13 14 16 17 19 21 22 24 25 27
4 5 6 7 9 10 11 12 13 15 16 17 18
7
.05
.01
1
--
3
0
5
1
6
3
8
4
10 12 14 16 18 20 22 24 26 28 30 32 34
6 7 9 10 12 13 15 16 18 19 21 22 24
8
.05
.01
2
--
4
I
6
2
8
4
10 13 15 17 19 22 24 26 29 31 34 36 38 41
6 7 9 11 13 15 17 18 20 22 24 26 28 30
9
.05
.01
2
0
4
I
7
3
10 12 15 17 20 23 26 28 31 34 37 39 42 45 48
5 7 9 11 13 16 18 20 22 24 27 29 31 33 36
10
.05
.01
3
0
5
2
8
4
I I 14 17 20 23 26 29 33 36 39 42 45 48 52 55
6 9 11 13 16 18 21 24 26 29 31 34 37 39 42
11
.05
.01
3
0
6
2
9
5
13 16 19 23 26 30 33 37 40 44 47 51 55 58 62
7 10 13 16 18 21 24 27 30 33 36 39 42 45 48
12
.05
.01
4
I
7
3
11 14 18 22 26 29 33 37 41 45 49 53 57 61 65 69
6 9 12 15 18 21 24 27 31 34 37 41 44 47 51 54
.. 13
.05
.01
4
I
8
.)
12 16 20 24 28 33 37 41 45 50 54 59 63 67 72 76
7 10 13 17 20 24 27 31 34 38 42 45 49 53 56 60
14
.05
.01
5
I
9
4
13 17 22 26 31 36 40 45 50 55 59 64 67 74 78 83
7 11 15 18 22 26 30 34 38 42 46 50 54 58 63 67
15
.05
.01
5
2
10 14 19 24 29 34 39 44 49 54 59 64 70 75 80 85 90
5 8 12 16 20 24 29 33 37 42 46 51 55 60 64 69 73
16
.05
.01
6
2
II
5
15 21 26 31 37 42 47 53 59 64 70 75 81 86 92 98
9 13 18 22 27 31 36 41 45 50 55 60 65 70 74 79
17
.05
.01
6
2
11 17 22 28 34 39 45 51 57 63 67 75 81 87 93 99 105
6 10 15 19 24 29 34 39 44 49 54 60 65 70 75 81 86
18
.05
.01
7
2
12 18 24 30 36 42 48 55 61 67 74 80 86 93 99 106 112
6 11 16 21 26 31 37 42 47 53 58 64 70 75 81 87 92
19
.05
.01
7
3
13 19 25 32 38 45 52 58 65 72 78 85 92 99 106 113 119
7 12 17 22 28 33 39 45 51 56 63 69 74 81 87 93 99
20
.05
.01
8
3
14 20 27 34 41 48 55 62 69 76 83 90 98 105 112 119 127
8 13 18 24 30 36 42 48 54 60 67 73 79 86 92 99 105
|
|
10 Page 10 |
▲back to top |
F Table for alpha=0.05
df2/dfl
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
40
60
120
Inf
I
1
161.4476
18.5128
10.128
7.7086
6.6079
2
199.5
19
9.5521
6.9443
5.7861
3
215.7073
19.1643
9.2766
6.5914
5.4095
4
224.5832
19.2468
9.1172
6.3882
5.1922
5
230.1619
19.2964
9.0135
6.2561
5.0503
6
233.986
19.3295
8.9406
6.1631
4.9503
7
236.7684
19.3532
8.8867
6.0942
4.8759
8
238.8827
19.371
8.8452
6.041
4.8183
9
240.5433
19.3848
8.8123
5.9988
4.7725
10
241.8817
19.3959
8.7855
5.9644
4.7351
12
243.906
19.4125
8.7446
5.9117
4.6777
15
245.9499
19.4291
8.7029
5.8578
4.6188
20
248.0131
19.4458
8.6602
5.8025
4.5581
24
249.0518
19.4541
8.6385
5.7744
4.5272
30
250.0951
19.4624
8.6166
5.7459
4.4957
40
251.1432
19.4707
8.5944
5.717
4.4638
60
252.1957
19.4791
8.572
5.6877
4.4314
120
253.2529
19.4874
8.5494
5.6581
4.3985
INF
254.3144
19.4957
8.5264
5.6281
4.365
5.9874
5.5914
5.3177
5.1174
4.9646
5.1433
4.7374
4.459
4.2565
4.1028
4.7571
4.3468
4.0662
3.8625
3.7083
4.5337
4.1203
3.8379
3.6331
3.478
4.3874
3.9715
3.6875
3.4817
3.3258
4.2839
3.866
3.5806
3.3738
3.2172
4.2067
3.787
3.5005
3.2927
3.1355
4.1468
3.7257
3.4381
3.2296
3.0717
4.099
3.6767
3.3881
3.1789
3.0204
4.06
3.6365
3.3472
3.1373
2.9782
3.9999
3.5747
3.2839
3.0729
2.913
3.9381
3.5107
3.2184
3.0061
2.845
3.8742
3.4445
3.1503
2.9365
2.774
3.8415
3.4105
3.1152
2.9005
2.7372
3.8082
3.3758
3.0794
2.8637
2.6996
3.7743
3.3404
3.0428
2.8259
2.6609
3.7398
3.3043
3.0053
2.7872
2.6211
3.7047
3.2674
2.9669
2.7475
2.5801
3.6689
3.2298
2.9276
2.7067
2.5379
4.8443
4.7472
4.6672
4.6001
4.5431
3.9823
3.8853
3.8056
3.7389
3.6823
3.5874
3.4903
3.4105
3.3439
3.2874
3.3567
3.2592
3.1791
3.1122
3.0556
3.2039
3.1059
3.0254
2.9582
2.9013
3.0946
2.9961
2.9153
2.8477
2.7905
3.0123
2.9134
2.8321
2.7642
2.7066
2.948
2.8486
2.7669
2.6987
2.6408
2.8962
2.7964
2.7144
2.6458
2.5876
2.8536
2.7534
2.671
2.6022
2.5437
2.7876
2.6866
2.6037
2.5342
2.4753
2.7186
2.6169
2.5331
2.463
2.4034
2.6464
2.5436
2.4589
2.3879
2.3275
2.609
2.5055
2.4202
2.3487
2.2878
2.5705
2.4663
2.3803
2.3082
2.2468
2.5309
2.4259
2.3392
2.2664
2.2043
2.4901
2.3842
2.2966
2.2229
2.1601
2.448
2.341
2.2524
2.1778
2.1141
2.4045
2.2962
2.2064
2.1307
2.0658
4.494
4.4513
4.4139
4.3807
4.3512
3.6337
3.5915
3.5546
3.5219
3.4928
3.2389
3.1968
3.1599
3.1274
3.0984
3.0069
2.9647
2.9277
2.8951
2.8661
2.8524
2.81
2.7729
2.7401
2.7109
2.7413
2.6987
2.6613
2.6283
2.599
2.6572
2.6143
2.5767
2.5435
2.514
2.5911
2.548
2.5102
2.4768
2.4471
2.5377
2.4943
2.4563
2.4227
2.3928
2.4935
2.4499
2.4117
2.3779
2.3479
2.4247
2.3807
2.3421
2.308
2.2776
2.3522
2.3077
2.2686
2.2341
2.2033
2.2756
2.2304
2.1906
2.1555
2.1242
2.2354
2.1898
2.1497
2.1141
2.0825
2.1938
2.1477
2.1071
2.0712
2.0391
2.1507
2.104
2.0629
2.0264
1.9938
2.1058
2.0584
2.0166
1.9795
1.9464
2.0589
2.0107
1.9681
1.9302
1.8963
2.0096
1.9604
1.9168
1.878
1.8432
4.3248
4.3009
4.2793
4.2597
4.2417
3.4668
3.4434
3.4221
3.4028
3.3852
3.0725
3.0491
3.028
3.0088
2.9912
2.8401
2.8167
2.7955
2.7763
2.7587
2.6848
2.6613
2.64
2.6207
2.603
2.5727
2.5491
2.5277
2.5082
2.4904
2.4876
2.4638
2.4422
2.4226
2.4047
2.4205
2.3965
2.3748
2.3551
2.3371
2.366
2.3419
2.3201
2.3002
2.2821
2.321
2.2967
2.2747
2.2547
2.2365
2.2504
2.2258
2.2036
2.1834
2.1649
2.1757
2.1508
2.1282
2.1077
2.0889
2.096
2.0707
2.0476
2.0267
2.0075
2.054
2.0283
2.005
1.9838
1.9643
2.0102
1.9842
1.9605
1.939
1.9192
1.9645
1.938
1.9139
1.892
1.8718
1.9165
1.8894
1.8648
1.8424
1.8217
1.8657
1.838
1.8128
1.7896
1.7684
1.8117
1.7831
1.757
1.733
1.711
4.2252
4.21
4.196
4.183
4.1709
3.369
3.3541
3.3404
3.3277
3.3158
2.9752
2.9604
2.9467
2.934
2.9223
2.7426
2.7278
2.7141
2.7014
2.6896
2.5868
2.5719
2.5581
2.5454
2.5336
2.4741
2.4591
2.4453
2.4324
2.4205
2.3883
2.3732
2.3593
2.3463
2.3343
2.3205
2.3053
2.2913
2.2783
2.2662
2.2655
2.2501
2.236
2.2229
2.2107
2.2197
2.2043
2.19
2.1768
2.1646
2.1479
2.1323
2.1179
2.1045
2.0921
2.0716
2.0558
2.0411
2.0275
2.0148
1.9898
1.9736
1.9586
1.9446
1.9317
1.9464
1.9299
1.9147
1.9005
1.8874
1.901
1.8842
1.8687
1.8543
1.8409
1.8533
1.8361
1.8203
1.8055
1.7918
1.8027
1.7851
1.7689
1.7537
1.7396
1.7488
1.7306
1.7138
1.6981
1.6835
1.6906
1.6717
1.6541
1.6376
1.6223
4.0847
4.0012
3.9201
3.8415
3.2317
3.1504
3.0718
2.9957
2.8387
2.7581
2.6802
2.6049
2.606
2.5252
2.4472
2.3719
2.4495
2.3683
2.2899
2.2141
2.3359
2.2541
2.175
2.0986
2.249
2.1665
2.0868
2.0096
2.1802
2.097
2.0164
1.9384
2.124
2.0401
1.9588
1.8799
2.0772
1.9926
1.9105
1.8307
2.0035
1.9174
1.8337
1.7522
1.9245
1.8364
1.7505
1.6664
1.8389
1.748
1.6587
1.5705
1.7929
1.7001
1.6084
1.5173
1.7444
1.6491
1.5543
1.4591
1.6928
1.5943
1.4952
1.394
1.6373
1.5343
1.429
1.318
1.5766
1.4673
1.3519
1.2214
1.5089
1.3893
1.2539
1