 |
DAE702S - DESIGN AND ANALSIS OF EXPERIMENTS - 1ST OPP - NOVEMBER 2024 |
 |
1 Page 1 |
▲back to top |

nAmlBIA UnlVERSITY
OF SCIEnCEAno TECHnOLOGY
FacultoyfHealthN, atural
ResourceasndApplied
Sciences
Schoool f NaturalandApplied
Sciences
Departmentof Mathematics,
StatisticsandActuarialScience
-P
13JacksonKaujeuaStreet
Private Bag13388
Windhoek
NAMIBIA
T: +264612072913
E: msas@nust.na
W: www.nust.na
QUALIFICATION: Bachelor of Science in Applied Mathematics and Statistics
QUALIFICATION CODE: 07BSAM
LEVEL:7
COURSE:DESIGN AND ANALYSIS OF EXPERIMENTS
COURSECODE: DAE702S
DATE: NOVEMBER 2024
SESSION: 1
DURATION: 3 HOURS
MARKS: 100
FIRST OPPORTUNITY: EXAMINATION QUESTION PAPER
EXAMINER:
MODERATOR:
INSTRUCTIONS:
Dr D Ntirampeba, NUST
Dr P liyambo, UNAM
1. Answer all questions on the separate answer sheet.
2. Please write neatly and legibly.
3. Do not use the left side margin of the answer sheet. This must be allowed for the
examiner.
4. No books, notes and other additional aids are allowed.
5. Write all answers clearly with their respective question numbers.
PERMISSIBLE MATERIALS:
1. Non-Programmable Calculator
ATTACHEMENTS
1. F Table & t-Table
This paper consists of 2 pages excluding this front page
 |
2 Page 2 |
▲back to top |

Question 1 (25 marks]
1.1 Briefly explain the following terrniuologies as they are applied to Experimental
Analysis of Variance.
(i) Experimental design
(ii) Treatment factor
(iii) Nuisance factor
(iv) One factor-at-a-time(OFAT) experimentation strategy
(v) Response surface
Design and
[2]
[2]
[2]
[2]
[2]
1.2 Consider the Analysis of Variance One Way Layout Design.
(i) Provide an appropriate effects model for this design.
[5]
(ii) Show that the total variability (SST) can be broken into two components, namely sum
of squares due treatment (SStreatment)and sum of squares due to errors (SSE),
[10]
Question 2 (25 marks]
2.1 Suppose the yield of a certain process is a function of X 1 and X 2 given by
where f is unknown and E represents the noise y.
(i) Use the two-term Taylor series approximation to approximate f near the point (x10,x20).
Write the obtained approximation in a form of a quadratic model
[8]
(ii) Generalize the quadratic model when k factors or independent variables are used [2]
2.2 A sample of a large government subsidized corporation consists of three virtually identical
plants. The government commissions a productivity investigation by the Department of
Labour at each of these plants. The investigation is carried out by random selection of a
number of workers at each plant. These workers are then subjected to intense tests and
questioning to determine their productivity. Since age affects productivity, the investigators
decide to include the age factor. The following table shows the productivity (%) of fifteen
workers. The measurements are given as indices with 100 representing a normal productivity.
Plant
Plant 1
Plant 2
Plant 3
18-19
103
110
89
20-24
114
112
Missing
Age
25-34
122
114
96
35-44
102
91
81
45-65
96
95
75
(i) Suggest an appropriate design for the data, justifying your choice.
[2]
(ii) Estimate the missing value.
[3]
(iii) ·would you say that there is a difference in the mean productivity of workers in the three
plants? Use a: = 0.05.
[10]
1
 |
3 Page 3 |
▲back to top |

- --
---
------------
Question 3 [20 marks]
An experiment is conducted to study the influence of operating temperature and three types
of face-plate glass the light output of an oscilloscope. The data are collected and presented in the
following table.
Temperature
Glass type 100
125 150
580
1090 1392
1 568
1087 1380
570
1085 1386
550
2 530
579
1070 1328
1035 1312
1000 1299
546
3 575
599
1045 867
1053 904
1066 889
3.1 Analyse the data to test the main effects of the glass type and temperature .
[15]
3.2 Is there a significant interaction between plate glass type and temperature? Use a= 0.05.[5]
Question 4 [30 marks]
4.1 Derive the formulae for the effects of A, B, and AB for a factorial design with two factors A
~B.
4.2 A router is used in locating notches on a printing circuit board. The vibration level at the
surface of the board as it is cut is considered to be a major source of dimensional variation
in notches. Two factors are thought to influence vibration: bit size (A) and cutting speed
(B). Two bit sizes ( /6 and ½inch ) and two speeds ( 40 and 90 rpm) are selected, and four
boards are cut at each set of conditions shown below.
Treatment
Replicate
A B combination
I II
III IV
(1) 18.2 18.9
12.9 14.4
+
-+
++
a 27.2 24
b 15.9 14.5
ab 41.0 43.9
22.4 22.5
15.1 14.2
36.3 39.9
(i) Use the formulae derived in (4.1) to calculate the effects of A, B, and AB. Interpret
the results
[6]
(ii) Use 0% significance level t.o t.est. the main effects of A and B, and the interaction effect.
AB.
[18]
END OF QUESTION PAPER
2
 |
4 Page 4 |
▲back to top |
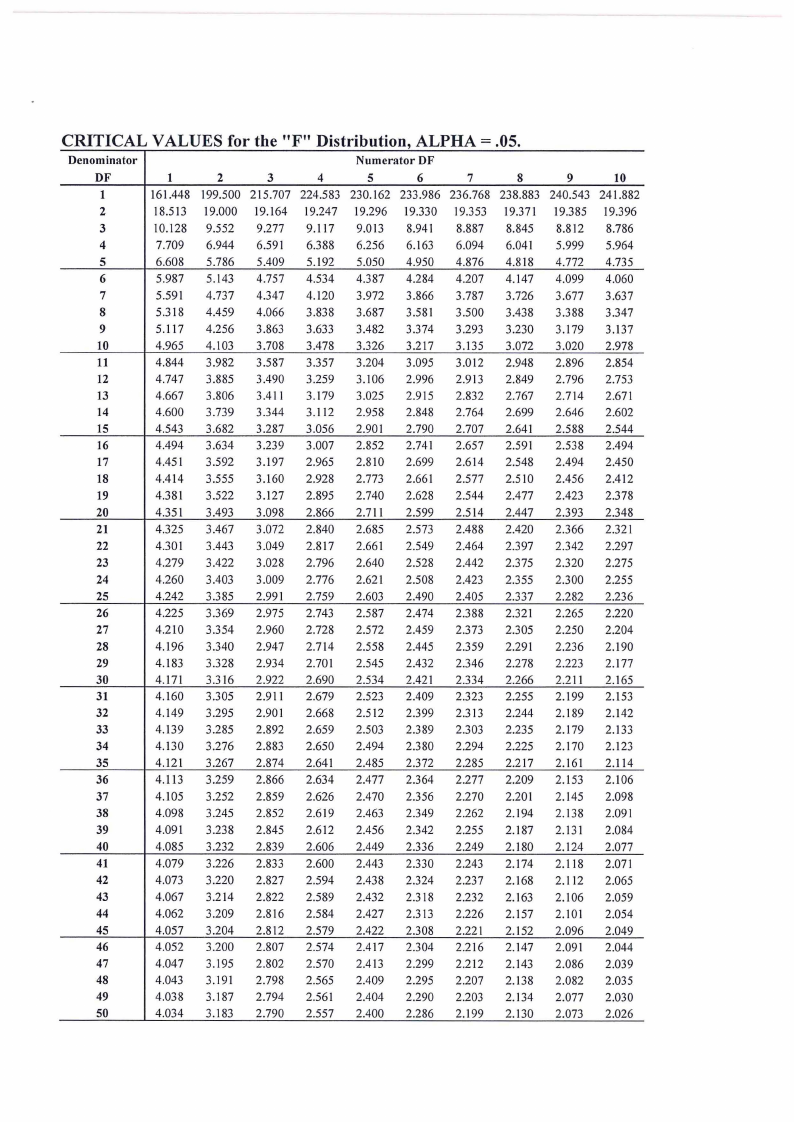
CRITICAL VALUES for the "F" Distribution, ALPHA= .05.
Denominator
Numerator DF
DF
1
2
3
4
5
6
7
8
1
161.448 199.500 215.707 224.583 230.162 233.986 236.768 238.883
2
18.513 19.000 19.164 19.247 19.296 19.330 19.353 19.371
3
10.128 9.552 9.277 9.117 9.013 8.941 8.887 8.845
4
7.709 6.944 6.591 6.388 6.256 6.163 6.094 6.041
5
6.608 5.786 5.409 5.192 5.050 4.950 4.876 4.818
6
5.987 5.143 4.757 4.534 4.387 4.284 4.207 4.147
7
5.591 4.737 4.347 4.120 3.972 3.866 3.787 3.726
8
5.318 4.459 4.066 3.838 3.687 3.581 3.500 3.438
9
5.117 4.256 3.863 3.633 3.482 3.374 3.293 3.230
10
4.965 4.103 3.708 3.478 3.326 3.217 3.135 3.072
11
4.844 3.982 3.587 3.357 3.204 3.095 3.012 2.948
12
4.747 3.885 3.490 3.259 3.106 2.996 2.913 2.849
13
4.667 3.806 3.411 3.179 3.025 2.915 2.832 2.767
14
4.600 3.739 3.344 3.112 2.958 2.848 2.764 2.699
15
4.543 3.682 3.287 3.056 2.901 2.790 2.707 2.641
16
4.494 3.634 3.239 3.007 2.852 2.741 2.657 2.591
17
4.451 3.592 3.197 2.965 2.810 2.699 2.614 2.548
18
4.414 3.555 3.160 2.928 2.773 2.661 2.577 2.510
19
4.381 3.522 3.127 2.895 2.740 2.628 2.544 2.477
20
4.351 3.493 3.098 2.866 2.711 2.599 2.514 2.447
21
4.325 3.467 3.072 2.840 2.685 2.573 2.488 2.420
22
4.301 3.443 3.049 2.817 2.661 2.549 2.464 2.397
23
4.279 3.422 3.028 2.796 2.640 2.528 2.442 2.375
24
4.260 3.403 3.009 2.776 2.621 2.508 2.423 2.355
25
4.242 3.385 2.991 2.759 2.603 2.490 2.405 2.337
26
4.225 3.369 2.975 2.743 2.587 2.474 2.388 2.321
27
4.210 3.354 2.960 2.728 2.572 2.459 2.373 2.305
28
4.196 3.340 2.947 2.714 2.558 2.445 2.359 2.291
29
4.183 3.328 2.934 2.701 2.545 2.432 2.346 2.278
30
4.171 3.316 2.922 2.690 2.534 2.421 2.334 2.266
31
4.160 3.305 2.911 2.679 2.523 2.409 2.323 2.255
32
4.149 3.295 2.901 2.668 2.512 2.399 2.313 2.244
33
4.139 3.285 2.892 2.659 2.503 2.389 2.303 2.235
34
4.130 3.276 2.883 2.650 2.494 2.380 2.294 2.225
35
4.121 3.267 2.874 2.641 2.485 2.372 2.285 2.217
36
4.113 3.259 2.866 2.634 2.477 2.364 2.277 2.209
37
4.105 3.252 2.859 2.626 2.470 2.356 2.270 2.201
38
4.098 3.245 2.852 2.619 2.463 2.349 2.262 2.194
39
4.091 3.238 2.845 2.612 2.456 2.342 2.255 2.187
40
4.085 3.232 2.839 2.606 2.449 2.336 2.249 2.180
41
4.079 3.226 2.833 2.600 2.443 2.330 2.243 2.174
42
4.073 3.220 2.827 2.594 2.438 2.324 2.237 2.168
43
4.067 3.214 2.822 2.589 2.432 2.318 2.232 2.163
44
4.062 3.209 2.816 2.584 2.427 2.313 2.226 2.157
45
4.057 3.204 2.812 2.579 2.422 2.308 2.221 2.152
46
4.052 3.200 2.807 2.574 2.417 2.304 2.216 2.147
47
4.047 3.195 2.802 2.570 2.413 2.299 2.212 2.143
48
4.043 3.191 2.798 2.565 2.409 2.295 2.207 2.138
49
4.038 3.187 2.794 2.561 2.404 2.290 2.203 2.134
so
4.034 3.183 2.790 2.557 2.400 2.286 2.199 2.130
9
240.543
19.385
8.812
5.999
4.772
4.099
3.677
3.388
3.179
3.020
2.896
2.796
2.714
2.646
2.588
2.538
2.494
2.456
2.423
2.393
2.366
2.342
2.320
2.300
2.282
2.265
2.250
2.236
2.223
2.211
2.199
2.189
2.179
2.170
2.161
2.153
2.145
2.138
2.131
2.124
2.118
2.112
2.106
2.101
2.096
2.091
2.086
2.082
2.077
2.073
10
241.882
19.396
8.786
5.964
4.735
4.060
3.637
3.347
3.137
2.978
2.854
2.753
2.671
2.602
2.544
2.494
2.450
2.412
2.378
2.348
2.321
2.297
2.275
2.255
2.236
2.220
2.204
2.190
2.177
2.165
2.153
2.142
2.133
2.123
2.114
2.106
2.098
2.091
2.084
2.077
2.071
2.065
2.059
2.054
2.049
2.044
2.039
2.035
2.030
2.026
 |
5 Page 5 |
▲back to top |
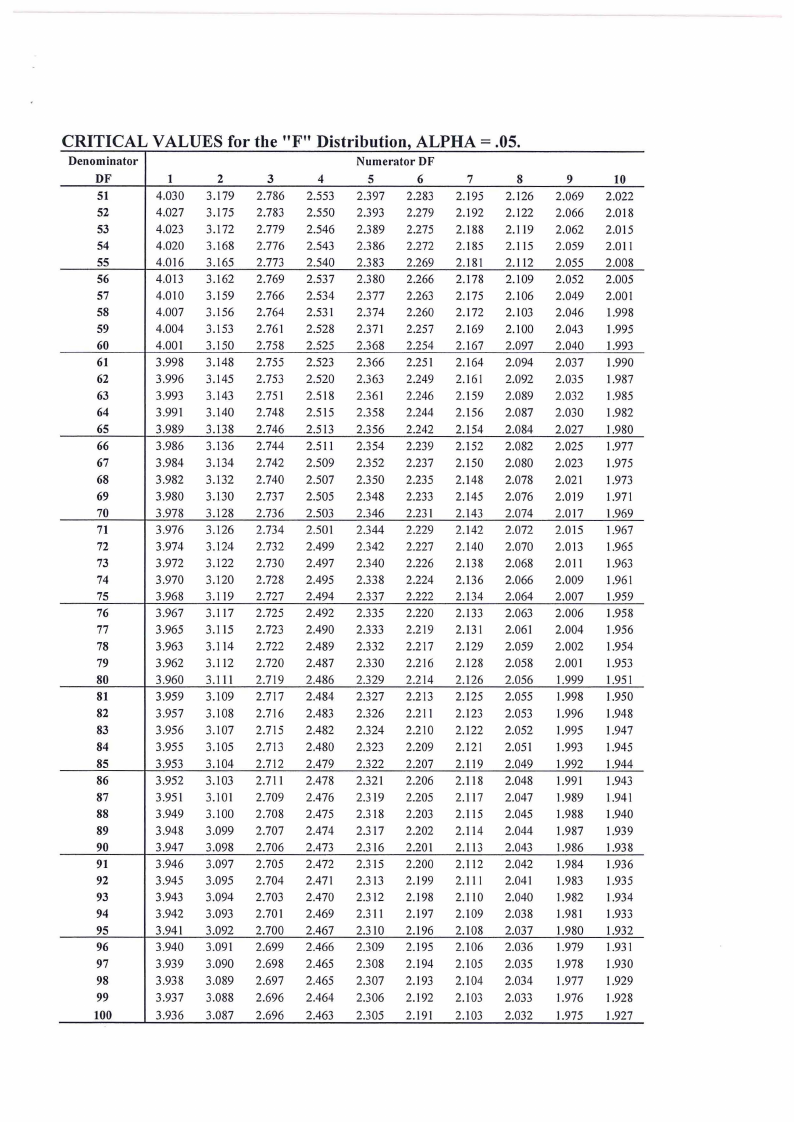
CRITICAL VALUES for the "F" Distribution, ALPHA=
Denominator
Numerator DF
DF
1
2
3
4
5
6
7
51
4.030 3.179 2.786 2.553 2.397 2.283 2.195
52
4.027 3.175 2.783 2.550 2.393 2.279 2.192
53
4.023 3.172 2.779 2.546 2.389 2.275 2.188
54
4.020 3.168 2.776 2.543 2.386 2.272 2.185
55
4.016 3.165 2.773 2.540 2.383 2.269 2.181
56
4.013 3.162 2.769 2.537 2.380 2.266 2.178
57
4.010 3.159 2.766 2.534 2.377 2.263 2.175
58
4.007 3.156 2.764 2.531 2.374 2.260 2.172
59
4.004 3.153 2.761 2.528 2.371 2.257 2.169
60
4.001 3.150 2.758 2.525 2.368 2.254 2.167
61
3.998 3.148 2.755 2.523 2.366 2.251 2.164
62
3.996 3.145 2.753 2.520 2.363 2.249 2.161
63
3.993 3.143 2.751 2.518 2.361 2.246 2.159
64
3.991 3.140 2.748 2.515 2.358 2.244 2.156
65
3.989 3.138 2.746 2.513 2.356 2.242 2.154
66
3.986 3.136 2.744 2.511 2.354 2.239 2.152
67
3.984 3.134 2.742 2.509 2.352 2.237 2.150
68
3.982 3.132 2.740 2.507 2.350 2.235 2.148
69
3.980 3.130 2.737 2.505 2.348 2.233 2.145
70
3.978 3.128 2.736 2.503 2.346 2.231 2.143
71
3.976 3.126 2.734 2.501 2.344 2.229 2.142
72
3.974 3.124 2.732 2.499 2.342 2.227 2.140
73
3.972 3.122 2.730 2.497 2.340 2.226 2.138
74
3.970 3.120 2.728 2.495 2.338 2.224 2.136
75
3.968 3.119 2.727 2.494 2.337 2.222 2.134
76
3.967 3.117 2.725 2.492 2.335 2.220 2.133
77
3.965 3.115 2.723 2.490 2.333 2.219 2.131
78
3.963 3.114 2.722 2.489 2.332 2.217 2.129
79
3.962 3.112 2.720 2.487 2.330 2.216 2.128
80
3.960 3.111 2.719 2.486 2.329 2.214 2.126
81
3.959 3.109 2.717 2.484 2.327 2.213 2.125
82
3.957 3.108 2.716 2.483 2.326 2.211 2.123
83
3.956 3.107 2.715 2.482 2.324 2.210 2.122
84
3.955 3.105 2.713 2.480 2.323 2.209 2.121
85
3.953 3.104 2.712 2.479 2.322 2.207 2.119
86
3.952 3.103 2.711 2.478 2.321 2.206 2.118
87
3.951 3.101 2.709 2.476 2.319 2.205 2.117
88
3.949 3.100 2.708 2.475 2.318 2.203 2.115
89
3.948 3.099 2.707 2.474 2.317 2.202 2.114
90
3.947 3.098 2.706 2.473 2.316 2.201 2.113
91
3.946 3.097 2.705 2.472 2.315 2.200 2.112
92
3.945 3.095 2.704 2.471 2.313 2.199 2.111
93
3.943 3.094 2.703 2.470 2.312 2.198 2.110
94
3.942 3.093 2.701 2.469 2.311 2.197 2.109
95
3.941 3.092 2.700 2.467 2.310 2.196 2.108
96
3.940 3.091 2.699 2.466 2.309 2.195 2.106
97
3.939 3.090 2.698 2.465 2.308 2.194 2.105
98
3.938 3.089 2.697 2.465 2.307 2.193 2.104
99
3.937 3.088 2.696 2.464 2.306 2.192 2.103
100
3.936 3.087 2.696 2.463 2.305 2.191 2.103
.05.
8
2.126
2.122
2.119
2.115
2.112
2.109
2.106
2.103
2.100
2.097
2.094
2.092
2.089
2.087
2.084
2.082
2.080
2.078
2.076
2.074
2.072
2.070
2.068
2.066
2.064
2.063
2.061
2.059
2.058
2.056
2.055
2.053
2.052
2.051
2.049
2.048
2.047
2.045
2.044
2.043
2.042
2.041
2.040
2.038
2.037
2.036
2.035
2.034
2.033
2.032
9
2.069
2.066
2.062
2.059
2.055
2.052
2.049
2.046
2.043
2.040
2.037
2.035
2.032
2.030
2.027
2.025
2.023
2.021
2.019
2.017
2.015
2.013
2.01 I
2.009
2.007
2.006
2.004
2.002
2.001
1.999
1.998
1.996
1.995
1.993
1.992
1.991
1.989
1.988
1.987
1.986
1.984
1.983
1.982
1.981
1.980
1.979
1.978
1.977
1.976
1.975
10
2.022
2.018
2.015
2.011
2.008
2.005
2.001
1.998
1.995
1.993
1.990
1.987
1.985
1.982
1.980
1.977
1.975
1.973
1.971
1.969
1.967
1.965
1.963
1.961
1.959
1.958
1.956
1.954
1.953
1.951
1.950
1.948
1.947
1.945
1.944
1.943
1.941
1.940
1.939
1.938
1.936
1.935
1.934
1.933
1.932
1.931
1.930
1.929
1.928
1.927
 |
6 Page 6 |
▲back to top |
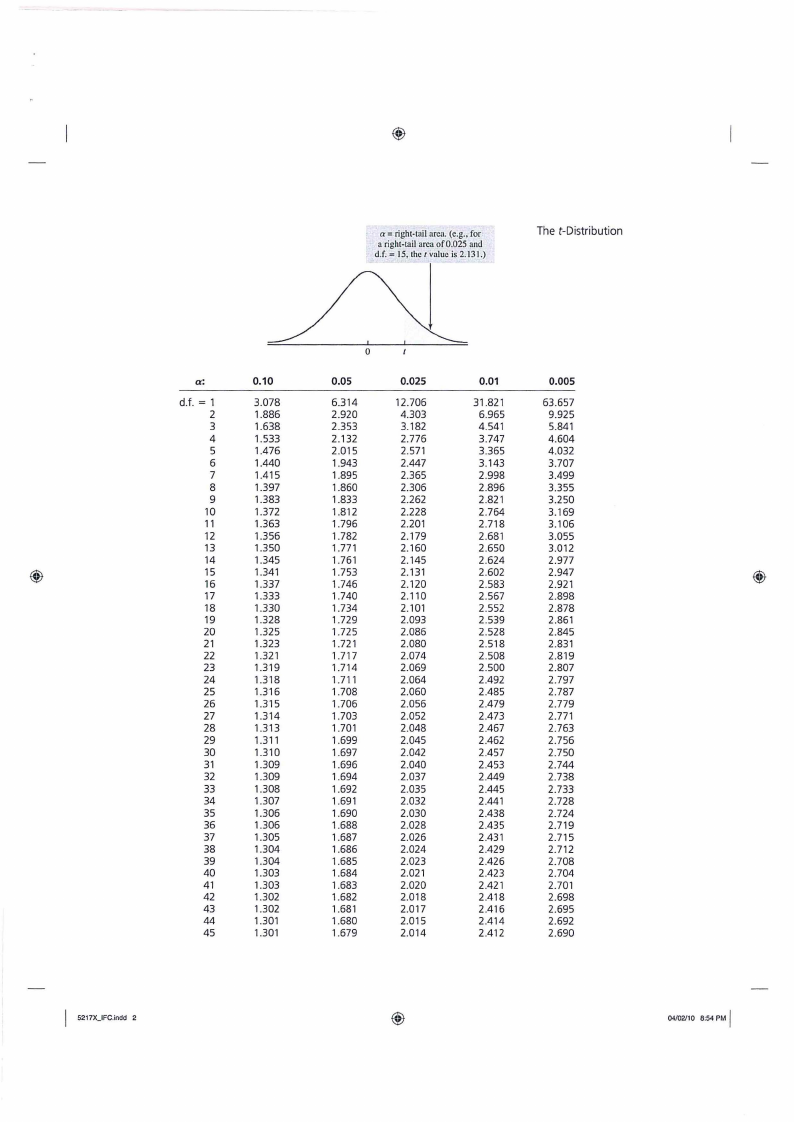
a= right-tail area. (e.g., for
a right-tail area of0.025 and
d.f. = 15, the I value is 2.131.)
The t-Distribution
a:
d.f. = 1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
0.10
3.078
1.886
1.638
1.533
1.476
1.440
1.415
1.397
1.383
1.372
1.363
1.356
1.350
1.345
1.341
1.337
1.333
1.330
1.328
1.325
1.323
1.321
1.319
1.318
1.316
1.315
1.314
1.313
1.311
1.310
1.309
1.309
1.308
1.307
1.306
1.306
1.305
1.304
1.304
1.303
1.303
1.302
1.302
1.301
1.301
0
0.05
6.314
2.920
2.353
2.132
2.015
1.943
1.895
1.860
1.833
1.812
1.796
1.782
1.771
1.761
1.753
1.746
1.740
1.734
1.729
1.725
1.721
1.717
1.714
1.711
1.708
1.706
1.703
1.701
1.699
1.697
1.696
1.694
1.692
1.691
1.690
1.688
1.687
1.686
1.685
1.684
1.683
1.682
1.681
1.680
1.679
0.025
12.706
4.303
3.182
2.776
2.571
2.447
2.365
2.306
2.262
2.228
2.201
2.179
2.160
2.145
2.131
2.120
2.110
2.101
2.093
2.086
2.080
2.074
2.069
2.064
2.060
2.056
2.052
2.048
2.045
2.042
2.040
2.037
2.035
2.032
2.030
2.028
2.026
2.024
2.023
2.021
2.020
2.018
2.017
2.015
2.014
0.01
31.821
6.965
4.541
3.747
3.365
3.143
2.998
2.896
2.821
2.764
2.718
2.681
2.650
2.624
2.602
2.583
2.567
2.552
2.539
2.528
2.518
2.508
2.500
2.492
2.485
2.479
2.473
2.467
2.462
2.457
2.453
2.449
2.445
2.441
2.438
2.435
2.431
2.429
2.426
2.423
2.421
2.418
2.416
2.414
2.412
0.005
63.657
9.925
5.841
4.604
4.032
3.707
3.499
3.355
3.250
3.169
3.106
3.055
3.012
2.977
2.947
2.921
2.898
2.878
2.861
2.845
2.831
2.819
2.807
2.797
2.787
2.779
2.771
2.763
2.756
2.750
2.744
2.738
2.733
2.728
2.724
2.719
2.715
2.712
2.708
2.704
2.701
2.698
2.695
2.692
2.690
5217X_IFC.indd 2
I 04/02/10 8:54 PM





